СОВРЕМЕННЫЙ КАЛЕНДАРЬ
Переход к программе пересчёта дат: http://razumru.ru/science/astronomy/krainev01.files/prog.htm
А. М. Крайнев
1. Астрономические основы построения календаря ↑
Календарь – это система обозначения и нумерации суток (календарных дат), отображающая периодичность происходящих на Земле сезонных изменений – весны, лета, осени, зимы. Основой для построения календаря являются два естественных периодических процесса – вращение Земли вокруг Солнца и вращение Земли вокруг собственной оси.
В астрономической литературе оба процесса как правило описываются в системе координат, связанной с земным наблюдателем, через воображаемое движение Солнца по воображаемой «небесной сфере». Такое описание формально безупречно, но не раскрывает сути механизма происходящего. В этом разделе в ущерб формальной безупречности сделана попытка дать некоторое наглядное представление об этом механизме. Следует иметь в виду, что на рис. 1, 5, 6, на которых одновременно изображена Земля и её орбита, Земля изображена в масштабах в 1500 – 2000 раз более крупном, чем масштаб, в котором изображена орбита. Изобразить на одном рисунке Землю и орбиту в реальных пропорциях невозможно, поскольку диаметр Земли (~12760 км) в 24000 раз меньше диаметра орбиты (~300 млн км), и при попытке изобразить их в одном масштабе, изображение Земли будет иметь размер сотых долей миллиметра. В результате на рис. 5 и 6 углы Δφ и Δω увеличены в ~15 раз.
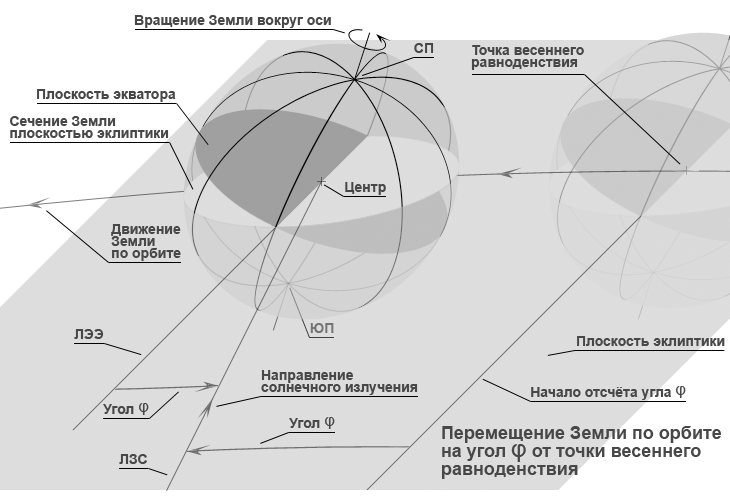
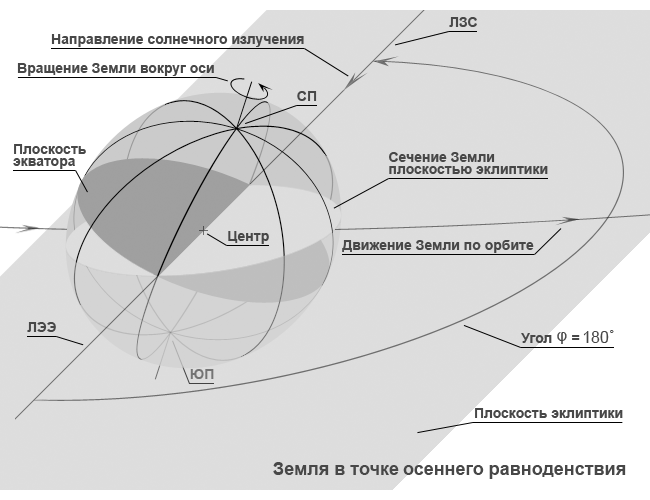
Тропический год. Сезонные изменения зависят от изменений количества солнечного тепла (включая все виды излучения), падающего на единицу площади земной поверхности в течение суток на широте конкретной местности. Это количество тепла определяется двумя факторами: высотой Солнца над горизонтом в течение светового дня и длительностью светового дня. Чем выше Солнце над горизонтом и чем длиннее световой день – тем больше тепла падает на единицу земной поверхности в течение суток. Не вдаваясь в подробности, можно сказать, что оба эти фактора зависят от угла φ между двумя прямыми, одна из которых – прямая пересечения плоскости земного экватора с плоскостью эклиптики (ЛЭЭ), вторая – прямая, соединяющая центры Земли и Солнца (ЛЗС), рис. 1 (эти прямые обозначены только для Земли, находящейся в положении «Угол φ»).
Если в плоскости эклиптики выбрать систему координат (x, y), начало которой расположить в центре Солнца, а ось x направить параллельно ЛЭЭ 1, то в любой точке земной орбиты угол между положительным направлением оси x и ЛЗС будет равен углу между ЛЭЭ и ЛЗС и может быть обозначен той же буквой φ. Если за начало отсчёта угла φ выбрать положительное направление оси x (φ = 0°), то при движении Земли по орбите угол φ будет равномерно 2 изменяться от 0° до 360°. Две характерные точки, в которых ЛЭЭ и ЛЗС совпадают между собой, а орбита Земли пересекает ось x, определяют моменты равноденствий. Для Северного полушария точка пересечения орбиты с положительным направлением оси x (φ = 0°) определяет момент весеннего равноденствия (положение «Весна» на рис. 1), а точка пересечения орбиты с отрицательным направлением оси x (φ = 180°) – момент осеннего равноденствия (положение «Осень» на рис. 1). Ещё двумя характерными точками являются точки пересечения орбиты Земли с осью y. Эти точки определяют моменты летнего и зимнего солнцестояний при φ = 90° и φ = 270° соответственно. На рис. 1 положения Земли во всех четырёх характерных точках для Северного полушария обозначены подписями «Весна», «Лето», «Осень», «Зима».
| |
|
|
| |
|
|
| |
|
|
| |
|
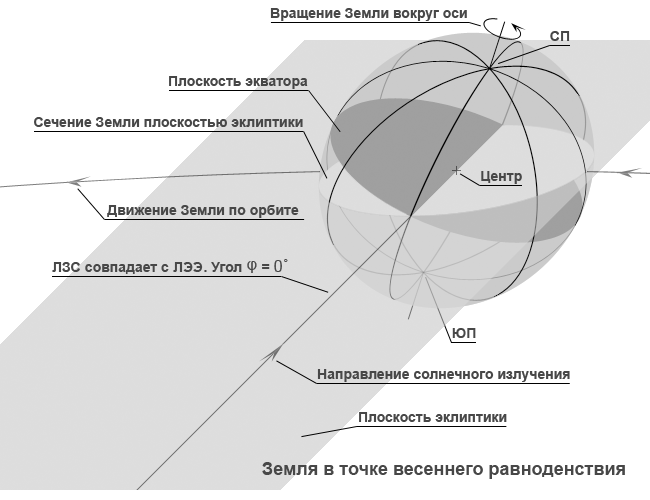
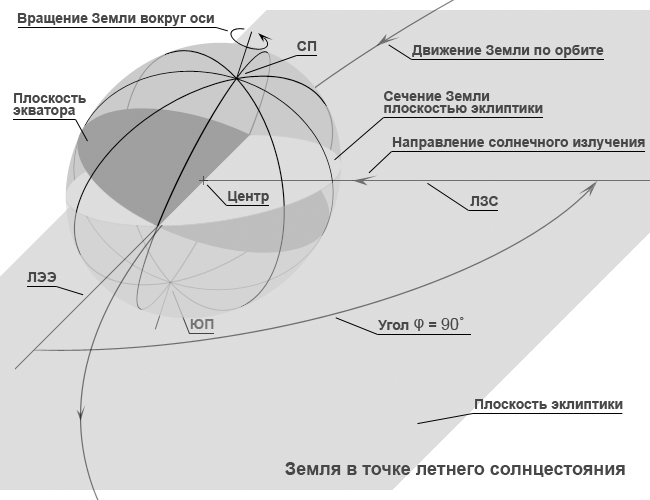
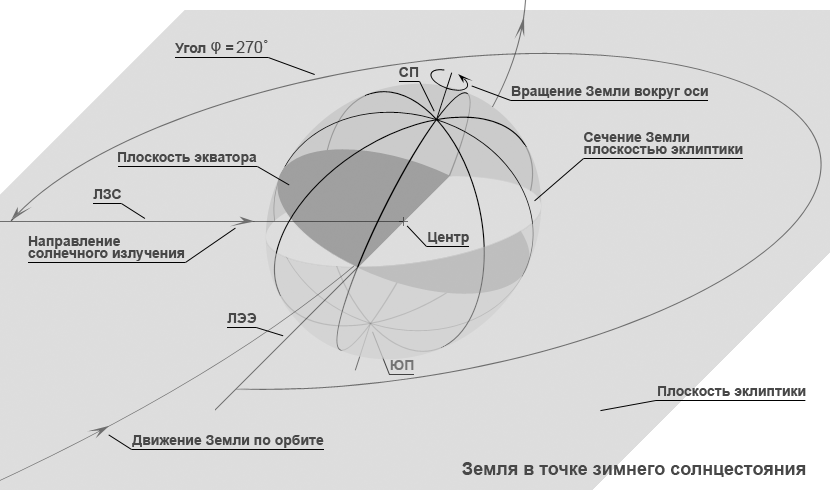
Рис. 1. Движение Земли по орбите и её положение в характерных точках в течение тропического года.
«Весна» – точка весеннего равноденствия, угол φ= 0°, начало отсчёта тропического года.
«Лето» – точка летнего солнцестояния, угол φ= 90°.
«Осень» – точка осеннего равноденствия, угол φ= 180°.
«Зима» – точка зимнего солнцестояния, угол φ= 270°.
«Угол φ» – перемещение Земли по орбите на произвольный угол φ от точки весеннего равноденствия.
Для увеличения масштаба навести курсор на изображение Земли.
Любой рисунок можно открыть в отдельном окне:
Основной рисунок, «Весна», «Лето», «Осень», «Зима», «Угол φ»
На основном рисунке Земля изображена в масштабе, увеличенном в ~1500 раз по сравнению с масштабом, в котором изображена земная орбита.
|
Период времени, требующийся для изменения угла φ от 0° до 360° (полный оборот Земли вокруг Солнца), называется тропическим годом.
Продолжительность тропического года, с точностью достаточной для наших целей, составляет 31556925 секунд. Эта величина изменяется очень медленно, и для построения календаря, охватывающего период в несколько тысяч лет, эти изменения пренебрежимо малы. Именно тропический год определяет периодичность сезонных изменений на Земле, которые и призван отображать календарь.
Продолжительность тропического года равную 31556925 секундам будем считать первой естественной исходной величиной для построения календаря.
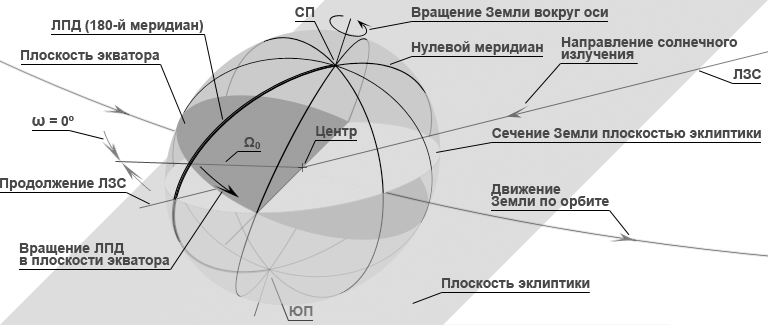
Средние солнечные сутки. Второй периодический процесс, на основе которого строится календарь, определяется вращением Земли вокруг собственной оси в плоскости экватора. Этот процесс можно охарактеризовать поворотом на угол ω прямой Ω, проведённой в плоскости экватора из центра Земли через 180-й меридиан, который называется линией перемены дат (ЛПД). За начало отсчёта угла ω = 0 выбирается направление прямой Ω0 в момент, когда ЛПД пересекает продолжение ЛЗС. В этот момент вдоль всей ЛПД наступает астрономическая полночь (00:00:00) и на ней начинается истечение новой даты, рис. 2.
 |
|
Рис. 2. Момент начала отсчёта угла ω = 0° и новой даты на ЛПД.
ЛПД (180-й меридиан) пересекает продолжение ЛЗС. На ЛПД астрономическая полночь – 00:00:00 новой даты. На всей остальной поверхности Земли, кроме ЛПД, предшествующая дата.
|
В результате осевого вращения Земли, ЛПД и прямая Ω вращаются в плоскости экватора в восточном направлении, угол ω увеличивается, а продолжение ЛЗС последовательно пересекают другие меридианы, расположенные к западу от ЛПД. В момент пересечения конкретным меридианом продолжения ЛЗС на этом конкретном меридиане наступает астрономическая полночь и тоже начинается истечение новой даты.
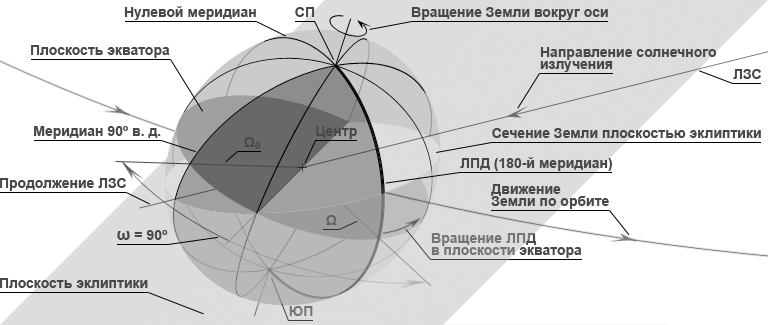
На рис. 3 показано положение Земли через 6 часов после наступления на ЛПД астрономической полночи (на ЛПД 06:00:00 утра). Прямая Ω повернулась в плоскости экватора от направления отсчёта Ω0 на угол ω = 90°. Во всём сегменте земной поверхности (затемнён) к западу от ЛПД до меридиана 90° в. д., в данный момент пересекающего продолжение ЛЗС, уже наступила новая дата. На остальной земной поверхности к востоку от ЛПД – предшествующая дата.
 |
|
Рис. 3. ЛПД и Ω повернулись в плоскости экватора на угол ω = 90° относительно направления отсчёта Ω0
На ЛПД – 06:00:00 утра. Продолжение ЛЗС пересекает меридиан 90° в. д. На этом меридиане астрономическая полночь – 00:00:00 новой даты. К западу от ЛПД до этого меридиана уже наступила новая дата (затемнённый сегмент). На всей остальной земной поверхности к востоку от ЛПД – предшествующая дата.
|
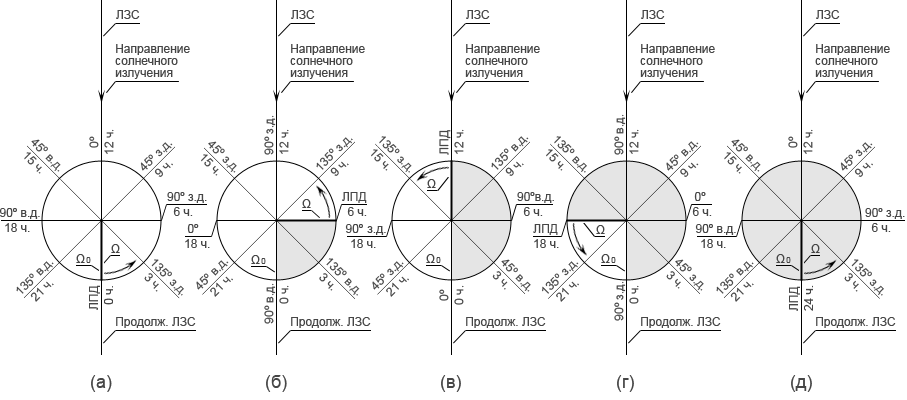
На рис. 4 показано развитие процесса перемены даты на различных меридианах в различные моменты времени при взгляде на Землю со стороны Северного полюса перпендикулярно плоскости экватора. Из рис. 3 и 4 видно, что ЛПД является границей, разделяющей всю земную поверхность на два шаровых сегмента, даты в которых различны: к западу от ЛПД – наступающая дата, к востоку – уходящая дата 3.
Далее, вращаясь вокруг земной оси, ЛПД вновь пересекает продолжение ЛЗС, рис. 4д. В этот момент на ЛПД вновь наступает полночь и начинается истечение следующей даты, а предшествующая дата превращается в уходящую. Весь цикл повторяется заново. Период времени между двумя ближайшими моментами, когда ЛПД пересекает продолжение ЛЗС, называется истинными солнечными сутками (ИСС).
 |
|
Рис. 4. Развитие процесса перемены даты на различных меридианах в Северном полушарии (вид на Северное полушарие перпендикулярно плоскости экватора)
(а) Момент появления на Земле новой даты. ЛПД пересекает продолжение ЛЗС. На ЛПД астрономическая полночь – 00:00:00 новой даты. Начало отсчёта угла ω = 0° прямые Ω и Ω0 совпадают. На всей земной поверхности, кроме ЛПД, предшествующая дата.
(б) Продолжение ЛЗС пересекает меридиан 90° в. д. На этом меридиане астрономическая полночь – 00:00:00 новой даты. Прямая Ω повернулась в плоскости экватора по отношению к прямой Ω0 на угол ω = 90°. На ЛПД 06:00:00 утра. На четверти земной поверхности к западу от ЛПД до меридиана 90° в. д. наступила новая дата (затемнённый сегмент). На остальной земной поверхности к востоку от ЛПД – предшествующая дата.
(в) Продолжение ЛЗС пересекает меридиан 0° (нулевой меридиан). На этом меридиане астрономическая полночь – 00:00:00 новой даты. Прямая Ω повернулась в плоскости экватора по отношению к прямой Ω0 на угол ω = 180°. На ЛПД астрономический полдень – 12:00:00. На половине земной поверхности к западу от ЛПД до нулевого меридиана наступила новая дата (затемнённый сегмент). На остальной земной поверхности к востоку от ЛПД – предшествующая дата.
(г) Продолжение ЛЗС пересекает меридиан 90° з. д. На этом меридиане астрономическая полночь – 00:00:00 новой даты. Прямая Ω повернулась в плоскости экватора по отношению к прямой Ω0 на угол ω = 270°. На ЛПД 18:00:00 вечера. На трёх четвертях земной поверхности к западу от ЛПД до меридиана 90° з. д. наступила новая дата (затемнённый сегмент). На остальной земной поверхности к востоку от ЛПД – предшествующая дата.
(д) Момент появления на Земле следующей даты. ЛПД вновь пересекает продолжение ЛЗС. На ЛПД астрономическая полночь – 24:00:00 даты, которая в данный момент превращается в уходящую, или 00:00:00 следующей даты. Прямые Ω и Ω0 вновь совпадают, начинается новый отсчёт угла ω = 0°. На всей земной поверхности, кроме ЛПД, – дата, которая в этот момент превращается в уходящую.
|
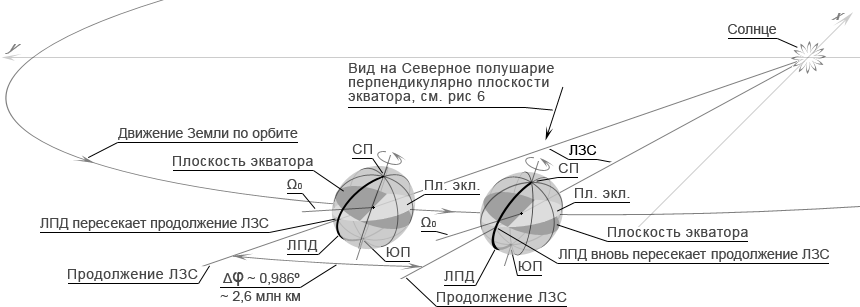
Но на суточное вращение Земли накладывается её орбитальное вращение. За период ИСС Земля перемещается по орбите на ~2,6 млн км и направление ЛЗС за это время изменяется на небольшой угол Δφ ~ 0,986°, рис. 5. Вследствие этого, прямая Ω0, от которой начинается отсчёт угла ω, за это время тоже поворачивается на угол Δω такого же порядка, как и угол Δφ. Поэтому каждое последующее пересечение ЛПД с продолжением ЛЗС происходит при повороте Земли вокруг оси на угол немного больший полного оборота: ωсут = 360°+ Δω, рис. 6 (на рис. 3 и 4 эти малые приращения углов Δφ и Δω не отображены). Следует отметить, что поворот ЛЗС происходит в плоскости эклиптики, а поворот Ω0 – в плоскости экватора. Поэтому как сами углы φ и ω, так и их приращения Δφ и Δω тоже измеряются в разных плоскостях – в плоскости эклиптики и в плоскости экватора соответственно.
 |
|
Рис. 5. Приращение Δφ угла φ за период ИСС
За период ИСС Земля перемещается по орбите на ~2,6 млн. км, а ЛЗС поворачивается на угол Δφ ~ 0,986° в плоскости эклиптики. Вследствие этого, прямая Ω0, от которой начинается отсчёт угла ω, тоже поворачивается на угол такого же порядка Δω ~ 0,986°, но – в плоскости экватора, см. рис 6.
Здесь Земля изображена в масштабе в ~1500 раз более крупном, а расстояние пройденное Землёй за сутки в масштабе в ~15 раз более крупном, чем масштаб расстояния от Земли до Солнца. Соответственно, и угол Δφ изображён увеличенным тоже в ~15 раз.
|
| |
|
 |
|
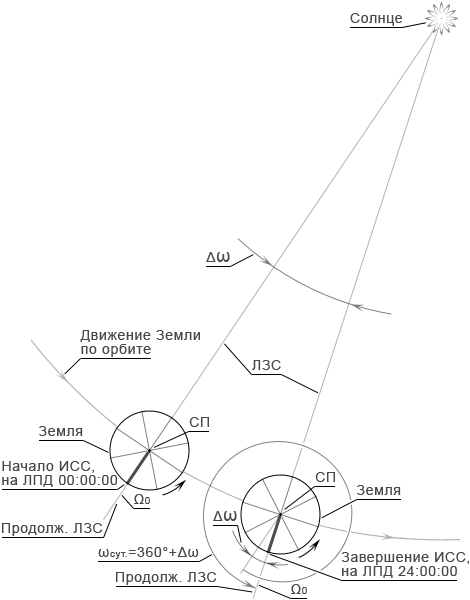
Рис. 6. Приращение Δω угла ω за период ИСС за счёт орбитального вращения Земли (вид на Северное полушарие перпендикулярно плоскости экватора)
За период ИСС прямая Ω0, от которой начинается отсчёт угла ω, поворачивается на угол Δω ~ 0,986°. В результате за период ИСС Земля поворачивается вокруг своей оси на угол немного больший полного оборота ωсут = 360°+ Δω.
Здесь Земля изображена в масштабе в ~2000 раз более крупном, чем масштаб расстояния от Земли до Солнца, а угол Δω – увеличенным в ~15 раз. Следует иметь в виду, что плоскость рисунка параллельна плоскости экватора, но не плоскости эклиптики. Поэтому рисунок представляет собой лишь проекции всех изображённых элементов на плоскость экватора. В этом ракурсе три прямые – Ω0, ЛПД и продолжение ЛЗС – сливаются в одну прямую.
|
|
В течение тропического года приращения Δφ и Δω колеблются около одного и того же среднего значения: Δφср. = Δωср. = 0,986°. Но характер этих колебаний различен. Вследствие эллиптичности земной орбиты Δφ колеблется с периодом равным тропическому году. Синфазно с ним колеблется и Δω. Но вследствие несовпадения экваториальной плоскости с плоскостью эклиптики, Δω колеблется ещё и с периодом равным половине тропического года. Между колебаниями этих двух видов Δω имеется сдвиг по фазе, зависящий от взаимного расположения осей эллипса орбиты и ЛЭЭ. Подробно анализировать эти процессы здесь не представляется возможным. Достаточно сказать, что суммарные колебания Δω приводят к тому, что продолжительность ИСС в течение тропического года тоже колеблется около своего среднего значения с амплитудой ~25 сек. Максимальная продолжительность ИСС наблюдается 22 декабря, минимальная (на 50 – 51 сек. короче) – 23 сентября. Таким образом, продолжительность ИСС – величина непостоянная.
Использовать сутки, продолжительность которых колеблется, неудобно. Поэтому в гражданском обиходе для исчисления суточного времени используются не ИСС, а период времени равный среднему значению ИСС, около которого и происходят колебания их продолжительности. Это значение так и называется – средние солнечные сутки. Продолжительность средних солнечных суток равна 24 часам или – 86400 секундам 4. Понятие ИСС в дальнейшем не понадобится, поэтому далее для краткости средние солнечные сутки будем называть просто «сутками».
Продолжительность суток равную 86400 секундам будем считать второй естественной исходной величиной для построения календаря.
2. Условная эра календарного исчисления ↑
Итак, имеют место два естественных периодических процесса, являющиеся основой календаря: тропический год (ТГ) продолжительностью 31556925 сек и сутки продолжительностью 86400 сек. Разделив продолжительность ТГ на продолжительность суток, получим продолжительность ТГ, выраженную в суточном измерении:
| T = 31556925 с / 86400 с ≈ 365,2422 сут |
(2.1) |
Всё было бы хорошо, если бы T оказалось целым числом. Но для построении календаря наличие дробной части доставляет массу неудобств. Дополнительные неудобства создают исторические предпосылки, встроенные в структуру календаря, но не вписывающиеся в десятичную систему счисления: деление года на 12 месяцев различной продолжительности и деление суток на 24 часа, а часа – на 60 минут и минуты – на 60 секунд. Поэтому, для построения календаря, который назовём «условным», в первую очередь отбросим эти исторические предпосылки. Не будем разбивать год на месяцы, а сутки – на часы и минуты, а для измерения времени будем применять только две единицы – сутки и ТГ, которые первоначально были определены через секунду – основную и самую мелкую единицу времени. Далее сосредоточимся на главном – на построении системы нумерации календарных дат таким образом, чтобы эта нумерация наглядно отображала повторяемость сезонных изменений и, по возможности, имела простую структуру.
Моменты времени, в которые Земля проходит через точки весеннего равноденствия, назовём сезонными реперными моментами. Один из таких моментов примем за нулевой, начнём от него отсчёт времени и построим шкалу текущего времени некоторой «условной эры» (УЭ) в отображении количества прошедших ТГ. В момент N = 0 начинается 1-й ТГ, который завершается в момент возврата Земли в точку весеннего равноденствия. На шкале времени момент завершения 1-го ТГ отобразится точкой с координатой N = 1 ТГ. При следующем возврате Земли в точку весеннего равноденствия завершается второй ТГ, что отобразится точкой с координатой N = 2 ТГ. Завершение третьего ТГ – точкой N = 3 ТГ. И т. д.
Нумеруя ТГ числами 1, 2, 3… N…, запишем, что в суточном отображении момент завершения N-го ТГ на шкале времени определится соотношением:
где N – количество ТГ, прошедших от начала УЭ; T = 365,2422 сут – продолжительность ТГ; t (NТГ) – момент завершения N-го ТГ от момента t = 0, выраженный в сутках.
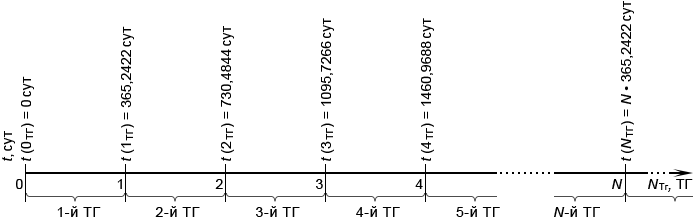
Шкала времени УЭ по порядковым номерам ТГ с отображением количества суток, прошедших к моменту завершения соответствующего ТГ, будет выглядеть как показано на рис. 7 и в табл. 1.
 |
| Табл. 1 |
| NТГ |
t (NТГ), сут |
| 1 |
t (1ТГ) = 365,2422 |
| 2 |
t (2ТГ) = 2 • 365,2422 = 730,4844 |
| 3 |
t (3ТГ) = 3 • 365,2422 = 1095,7266 |
| 4 |
t (4ТГ) = 4 • 365,2422 = 1460,9688 |
| ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |
| N |
t (NТГ) = N • 365,2422 |
| ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |
|
| |
|
|
Рис. 7. Шкала времени УЭ
Единица измерения времени – ТГ,
NТГ – количество ТГ, прошедших от начала УЭ,
t (NТГ) – количество суток, прошедших к моменту завершения N-го ТГ.
|
|
Но удобнее шкала, на которой в качестве единицы измерения времени используется не ТГ, а сутки, рис. 8. Здесь шкала разбита на четыре части так, чтобы на ней более подробно отображался каждый из первых 4-х ТГ с небольшим продолжением на соседние ТГ. Части шкалы расположены одна под другой таким образом, чтобы моменты начала и завершения всех ТГ располагались на одних и тех же вертикалях (показаны пунктирами). В нулевой момент начинается истечение 1-х суток УЭ, что отображается точкой t = 0 сут, а их завершение и начало 2-х суток – точкой t = 1 сут. Момент завершения 2-х суток отображается точкой t = 2 сут. Момент завершения 3-х суток – точкой t = 3 сут. И т. д.
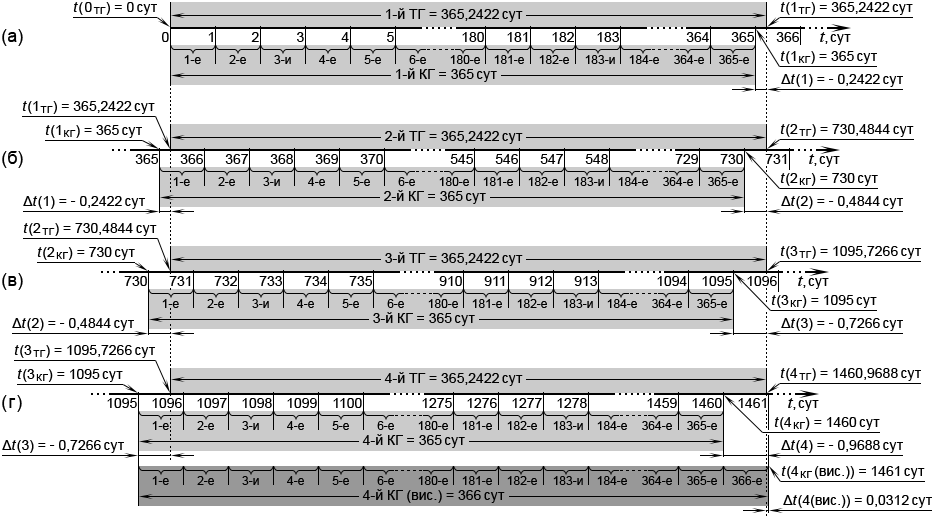
На протяжении 1-го ТГ шкала времени в суточном отображении будет выглядеть как показано на рис. 8а. Момент начала 1-го ТГ совпадает с моментом начала 1-х суток и отображается точкой t (0ТГ) = 0 сут. Момент завершения 1-го ТГ и начала 2-го ТГ отображается точкой t (1ТГ) = 365,2422 сут. Этот момент приходится на 366-е сутки и отстоит от их начала на величину 0,2422 сут, что составляет 5ч:48м:46,08с.
Если в календарном исчислении использовать естественную продолжительность ТГ, то 366-е сутки будут разбиты на две части: первая часть будет относиться к 1-му ТГ, вторая – ко 2-му ТГ. Такая структура календаря неудобна для гражданского обихода. Поэтому для определения продолжительности календарного года (КГ) целесообразно использовать период времени исчисляемый целым количеством суток и при этом по возможности приближенный к продолжительности ТГ. Наиболее близкое целое значение – 365 сут. Но в этом случае начало 2-го КГ смещается на более ранний момент по отношению к началу 2-го ТГ на величину 0,2422 сут. А поскольку продолжительность 2-го КГ тоже меньше продолжительности 2-го ТГ на такую же величину, то 2-й КГ завершится раньше 2-го ТГ уже на удвоенное её значение: 2 • 0,2422 = 0,4844 сут, рис. 8б. И т. д., момент завершения каждого последующего КГ будет и далее смещаться по отношению к моменту завершения соответствующего ТГ на более раннее время с шагом 0,2422 сут, рис. 8в, г.
 |
|
Рис. 8. Смещение по шкале времени первых 4-х КГ относительно первых 4-х ТГ
Единица измерения времени – сутки; t – текущее время в сутках от момента t = 0 сут.
Номерами под фигурными скобками пронумерованы сутки в пределах каждого КГ.
| (а) |
N = 1 |
t = 0 – 366 сут; |
| (б) |
N = 2 |
t = 365 – 731 сут; |
| (в) |
N = 3 |
t = 730 – 1096 сут; |
| (г) |
N = 4 |
t = 1095 – 1461 сут; |
| |
|
|
|
|
Если каждому ТГ, имеющему порядковый номер N (см. (2.2)), поставить в соответствие КГ с таким же номером, а момент завершения N-го КГ обозначить t (NКГ), то смещение Δt (N) момента завершения N-го КГ по отношению к моменту завершения N-го ТГ можно определить соотношением:
| Δt (N) = t (NКГ) – t (NТГ) |
(2.3) |
При одинаковой продолжительности K всех КГ моменты их завершения t (NКГ) определятся соотношением:
В этом случае, с учётом (2.2), соотношение (2.3) для смещения момента завершения Δt (N) можно переписать следующим образом:
| Δt (N) = t (NКГ) – t (NТГ) = N • (K – T ) |
(2.4) |
Подставив сюда принятое значение продолжительности КГ K = 365 сут и полученное из (2.1) значение продолжительности ТГ T = 365,2422 сут, найдём смещения моментов завершения N-х КГ по отношению к моментам завершения N-х ТГ при одинаковой продолжительности всех КГ равной 365 сут:
| Δt (N) = N • (365 – 365,2422) = – N • 0,2422 сут |
| |
Табл. 2 |
| |
| N |
t (NКГ), сут |
t (NТГ), сут |
Δt (N), сут |
| 1 |
365 |
365,2422 |
– 0,2422 |
| 2 |
730 |
730,4844 |
– 0,4844 |
| 3 |
1095 |
1095,7266 |
– 0,7266 |
| 4 |
1460 |
1460,9688 |
– 0,9688 |
| 4(в) |
1461 |
1460,9688 |
0,0312 |
| ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |
| 100 |
36500 |
36524,2200 |
– 24,2200 |
| 101 |
36865 |
36889,4622 |
– 24,4622 |
| 102 |
37230 |
37254,7044 |
– 24,7044 |
| 103 |
37595 |
37619,9466 |
– 24,9466 |
| 104 |
37960 |
37985,1888 |
– 25,1888 |
| ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |
|
Знак «минус» показывает, что в данном случае все КГ завершаются раньше, чем соответствующие ТГ, т. е. до момента завершения N-го КГ от начала УЭ проходит меньше времени, чем до момента завершения соответствующего N-го ТГ.
Подсчитаем значения t (NКГ), t (NТГ), Δt (N) для первых четырёх N и несколько значений для N ~100, табл. 2 (значения из первых пяти строк табл. 2 отображены на рис. 8). Начало 1-го КГ по определению УЭ было задано моментом весеннего равноденствия, но при сохранении продолжительности всех КГ в 365 сут уже начало 5-го КГ (соответствует моменту завершения 4-го КГ) смещается на более ранний момент почти на сутки (на 0,9866 сут), а для КГ, имеющих номера 100 и более, смещение достигает 24 – 25 сут.
Таким образом, календарь, в котором продолжительность всех КГ одинакова и составляет K = 365 сут, постепенно перестаёт выполнять свою функцию – на один и тот же сезонный реперный момент в разные КГ приходятся разные календарные даты. Понятно, что с дальнейшим ростом номеров КГ эта ошибка будет нарастать. Но корректный календарь должен быть структурирован таким образом, чтобы изначально заданное соответствие календарных дат и сезонных реперных моментов повторялось ежегодно на протяжении достаточно длительного (в идеале, неограниченного) исторического периода. И для того, чтобы синхронизовать календарные даты с сезонными реперными моментами, существует только один способ – подобрать такую структуру изменений продолжительности КГ при сохранении в каждом из них целого количества суток, чтобы моменты завершения всех КГ как можно меньше отклонялись от моментов завершения соответствующих ТГ. Эта задача решается методом последовательных приближений.
3. Структура юлианского календаря ↑
Первое приближение было найдено в 46 году до н. э.5 александрийским астрономом Созигеном. Он разработал простое правило: три КГ подряд должны иметь продолжительность равную 365 сут, а каждый 4-й КГ – 366 сут. Далее календарь должен строиться на основе повторения таких четырёхлетних циклов. Годы продолжительностью 365 сут называются простыми, а продолжительностью 366 сут – високосными. Это правило было введено в практику Юлием Цезарем. По его имени календарь такой структуры получил наименование юлианского календаря.
Применительно к первым четырём КГ УЭ эта структура отображена на рис. 8. Для каждого КГ под фигурными скобками приведена строка, содержащая порядковые номера суток, отсчитываемых от начала этого КГ. Первые три КГ содержат по 365 сут, а 4-й КГ – 366 сут. Для 4-го КГ (рис. 8г) обозначены моменты его завершения если бы этот КГ был простым t (4КГ) = 1460 сут, или, в соответствии с юлианской структурой, – високосным t (4КГ(в)) = 1461 сут. Високосный 4-й КГ затемнён интенсивнее, чем простые КГ. Момент t (4КГ(в)) отображён и в затемнённой строке табл. 2.
Но 4-й ТГ завершается в момент t (4ТГ) = 1460,9688 сут, а високосный 4-й КГ(в), определяющий момент завершения 1-го юлианского цикла, – в момент t (4КГ(в)) = 1461 сут (см. табл. 2 и рис. 8г). Таким образом, момент завершения 4-го КГ(в), скорректированного юлианским приближением, тоже не совпадает с моментом завершения 4-го ТГ. Его смещение составляет:
| Δt (4) = t (4КГ(в) ) – t (4ТГ) = 1461 сут – 1460,9688 сут = 0,0312 сут |
Смещение имеет знак «плюс». Это значит, что первый четырёхлетний календарный юлианский цикл завершается позже, чем первый четырёхлетний тропический цикл на 0,0312 сут. А поскольку каждый последующий четырёхлетний юлианский цикл тоже продолжительнее соответствующего четырёхлетнего тропического цикла на такую же величину, то моменты завершения четырёхлетних календарных юлианских циклов по отношению к моментам завершения соответствующих четырёхлетних тропических циклов и дальше будут смещаться на всё более позднее время с шагом 0,0312 сут.
Календарь, состоящий из КГ одинаковой продолжительности по 365 сут, за каждые четыре КГ смещался на 0,9688 сут (23ч:15м:4,32с) по отношению к четырём ТГ, а календарь юлианской структуры за каждые четыре КГ – всего лишь на 0,0312 сут (00ч:44м:55,68с). Тем не менее, пренебрегать этим смещением без оценки набегающей ошибки в течение длительного исторического периода не следует.
Проведём такую оценку. Но предварительно формализуем предшествующие рассуждения.
Определим максимально допустимое смещение календарных дат по отношению к сезонным реперным моментам из следующих соображений. В гражданском обиходе вместо словосочетаний «момент равноденствия» или «момент солнцестояния» употребляются словосочетания «день равноденствия» или «день солнцестояния». Таким образом, с т. з. обихода смещение календарных дат от реперных моментов в пределах 1 сут вполне допустимо. С другой стороны, поскольку КГ должен содержать целое количество суток, то 1 сут – это минимальная величина, на которую мы имеем возможность изменять его продолжительность. Исходя из этого, для того, чтобы календарь был приемлем и удобен в обиходе, вполне достаточно структурировать его таким образом, чтобы смещения календарных дат, которые выпадают на реперные моменты, лежали в пределах 1 сут по отношению к самим этим моментам. Значение равное 1 сут назовём критерием точности, а структуру календаря будем считать приемлемой для применения лишь на такой исторический период, пока смещение Δt (N), вне зависимости от его знака, не превысит величину 1 сут. Это условие можно записать следующим образом:
Исходя из этого, можно сформулировать правило корректировки календаря: корректировать на 1 сут следует КГ, номер которого имеет максимальное значение при удовлетворении соотношения (3.1). Корректировка должна производиться в сторону противоположную знаку смещения.
И это правило, и условие (3.1) не являются догмами. Можно принять и другие критерии точности, и сформулировать другие правила корректировки, которым будут соответствовать различные календарные структурные схемы, которые с той или иной степенью точности будут синхронизировать календарные даты с сезонными реперными моментами. Здесь во многом играют роль наглядность и простота применения той или иной схемы. Тем не менее, отметим, что сформулированное правило приводит к оптимальной структуре календаря, которая в сегодняшнем календаре не была реализована.
Поскольку Δt (N) является функцией N и по абсолютной величине растёт с ростом N, то заменив в (3.1) неравенство на равенство, получим уравнение относительно N, которое будет удовлетворять условию (3.1) при максимальном значении Nmax :
| | Δt (Nmax) | = 1 сут |
(3.2) |
В общем случае решение этого уравнения относительно Nmax не будет целочисленным, но номер КГ должен быть целым числом. Поэтому для нахождения номера КГ, подлежащего корректировке, надо округлить Nmax до ближайшего целого числа в меньшую сторону. Для такого округления удобно применить оператор «floor», используемый в программировании 6. Тогда номер КГ подлежащего корректировке определится соотношением:
Проиллюстрируем применение критерия точности и правила корректировки для получения юлианского приближения. Вернёмся к календарю, состоящему из КГ одинаковой продолжительности K = 365 сут и, подставив Δt (N) из (2.4) в условие (3.2) 7, найдём Nmax :
| Nmax • | K – T | = 1 сут |
| Nmax = 1 сут / | K – T | |
Подставив Nmax в (3.3), придём к соотношению:
| N = floor (Nmax) = floor (1 сут / | K – T |), |
подставив в которое численные значения K = 365 сут и T = 365,2422 сут, найдём номер КГ, подлежащего корректировке:
| N = floor (1 сут / | 365 сут – 365,2422 сут |) ≈ floor 4,129 = 4 |
Как следует из (2.4) и табл. 2, смещение Δt (N) отрицательно. Поэтому продолжительность КГ, имеющего номер N = 4, следует увеличить на 1 сут, что и соответствует структуре календаря в юлианском приближении.
Отметим, что структура календаря – это ещё не календарь. Чтобы структуру превратить в календарь, необходимо датировки, отображаемые этой структурой, привязать к конкретным историческим событиям. В этом смысле, календарь, утверждённый Юлием Цезарем, и календарь, который принято называть юлианским сегодня, – это разные календари. Юлианский календарь (ЮК) в современном понимании был разработан в 525 г. н. э. монахом Дионисием Малым. И хотя оба эти календаря имеют одинаковую юлианскую структуру, но их привязки к историческим событиям совершенно разные.
4. Оптимальные второе и третье приближения ↑
Вернёмся к оценке набегающей ошибки календаря юлианской структуры.
Значения моментов завершения любых КГ юлианского приближения можно записать используя уже знакомый оператор «floor»:
| t (NКГ) = N • K + floor (N / 4) |
(4.1) |
Первое слагаемое N • K в правой части (4.1) – это количество суток, содержащихся в N КГ, если бы все КГ были простыми продолжительностью K = 365 сут. Второе слагаемое floor (N / 4) – добавка в 1 сут на каждые 4 КГ, привносимая юлианским приближением.
Подставив (4.1) и (2.2) в (2.3), найдём временны́е смещения моментов завершения любых юлианских КГ относительно моментов завершения соответствующих ТГ:
| Δt (N) = t (NКГ) – t (NТГ) = N • K + floor (N / 4) – N • T = N • (K – T) + floor (N / 4) |
(4.2) |
При значениях N кратных 4 аргумент во втором слагаемом результирующей части (4.2) будет целочисленным. В этом случае будет выполняться равенство:
| floor (Nкр4 / 4) = Nкр4 / 4 |
и смещения моментов, завершающих юлианские циклы, определятся соотношением:
| Δt (Nкр4) = Nкр4 • (K – T) + Nкр4 / 4 = Nкр4 • (K – T + 1 / 4) |
(4.3) |
Соотношения (4.1) и (4.2) применимы к любым КГ календаря юлианской структуры в то время, как соотношение (4.3) – только к КГ, завершающим четырёхлетние юлианские циклы, номера которых кратны 4.
Применим принятый критерий корректировки аналогично тому, как это было сделано для нахождения юлианского приближения. Подставив Δt (Nкр4) из (4.3) в условие (3.2), получим уравнение для Nкр4 max :
| Nкр4 max• | K – T + 1 / 4 | = 1 сут, |
Переписав это уравнение относительно Nкр4 max и, в соответствии с (3.3), применив оператор «floor», получим целочисленное значение Nкр4 , удовлетворяющее критерию точности (3.1) и принятому правилу корректировки:
| Nкр4 = floor (1 сут / | K – T + 1 / 4 |) |
Подставив численные значения K = 365 сут и T = 365,2422 сут, найдём значение номера КГ, завершающего юлианский цикл и подлежащего корректировке во втором приближении:
| |
Табл. 3 |
| |
| N |
t (NКГ), сут |
t (NТГ), сут |
Δt (N), сут |
| 4(в) |
1461 |
1460,9688 |
0,0312 |
| 8(в) |
2922 |
2921,9376 |
0,0624 |
| ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |
| 124(в) |
45291 |
45290,0328 |
0,9672 |
| 128(в) |
46752 |
46751,0016 |
0,9984 |
| 128 |
46751 |
46751,0016 |
– 0,0016 |
|
| |
|
| Nкр4 = floor (1 сут / | 365 – 365,2422 + 1 / 4 |) ≈ floor 128,205 = 128 |
Из (4.3) легко установить, что смещения Δt (Nкр4) положительны (ранее уже было показано, что Δt (4) = 0,0312 сут), поэтому каждый 128-й КГ подлежит корректировке на 1 сут в сторону сокращения его продолжительности.
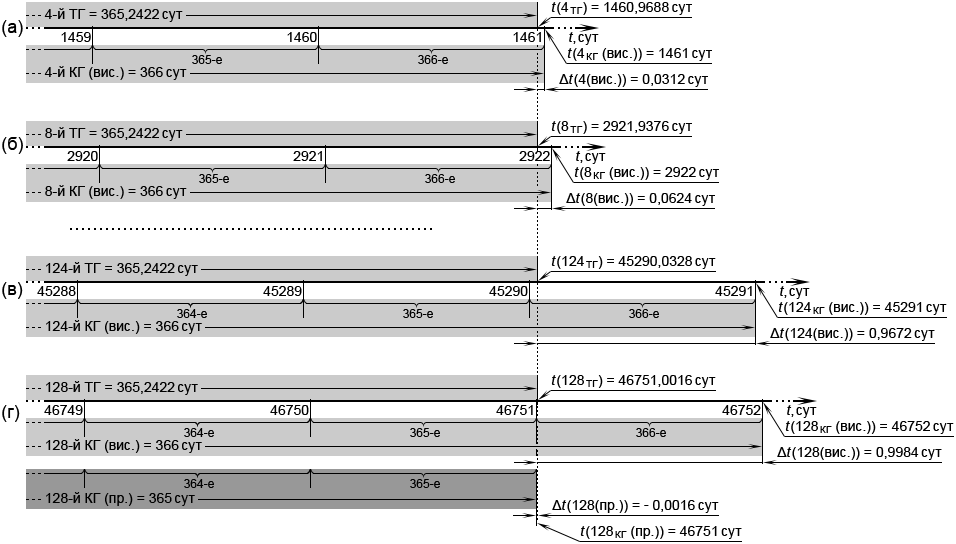
Отобразим процессы, описывающие вторую корректировку, на шкале времени. Используя соотношения (4.1) и (4.2), подсчитаем значения t (NКГ) и Δt (N) для КГ, имеющих номера 4, 8 и 124, 128 (они все кратны 4). Значения t (NТГ) для соответствующих номеров ТГ подсчитаем по (2.2). Результаты представлены в табл. 3 и отображены на рис. 9. Все КГ, отображённые в незатемнённых строках табл. 3, являются високосными, поскольку они завершают четырёхлетние юлианские циклы. Затемнённая строка табл. 3 отображает простой 128-й КГ, скорректированный вторым приближением в сторону его сокращения из високосного до простого. На рис. 9г этот, скорректированный до простого, 128-й КГ затемнён интенсивнее, чем високосные КГ.
 |
|
Рис. 9. Смещение по шкале времени юлианских циклов относительно тропических циклов
Единица измерения времени – сутки; t – текущее время в сутках от момента t = 0 сут.
Номерами под фигурными скобками пронумерованы сутки в пределах каждого КГ.
В связи с тем, что после первого (юлианского) приближения смещения Δt (N) существенно уменьшились, для того, чтобы отобразить их на рисунке, масштаб шкалы времени растянут в 5 раз по сравнению с масштабом, принятым на рис. 8. Поэтому удаётся отобразить лишь несколько суток, завершающих четырёхлетние циклы.
| (а) |
N = 4 |
t = 1459 – 1461 сут; |
| (б) |
N = 8 |
t = 2920 – 2922 сут; |
| (в) |
N = 124 |
t = 45288 – 45291 сут; |
| (г) |
N = 128 |
t = 46749 – 46752 сут; |
| |
|
|
|
|
Второе приближение уточняет юлианское правило следующим образом: три КГ подряд должны иметь продолжительность равную 365 сут, а каждый 4-й КГ, за исключением КГ, номера которых кратны 128, – 366 сут. Таким образом, КГ, номера которых кратны 128, должны оставаться простыми продолжительностью 365 сут, несмотря на то, что по юлианскому правилу они должны были бы быть високосными. Далее календарь должен строиться на основе повторения таких 128-летних циклов.
Моменты завершения любых КГ с учётом второго приближения можно записать уточнив соотношение (4.1) следующим образом:
| t (NКГ) = N • K + floor (N / 4) – floor (N / 128) |
(4.4) |
Последнее слагаемое имеет знак «минус», поскольку вторая корректировка производится в сторону уменьшения продолжительности КГ, кратных значению 128.
Подставив в (2.3) соотношения (4.4) и (2.2), найдём смещения моментов завершения любых КГ относительно моментов завершения соответствующих ТГ для календаря, построенного с учётом второго приближения:
| Δt (N) = t (NКГ) – t (NТГ) = N • K + floor (N / 4) – floor (N / 128) – N • T = N • (K – T) + floor (N / 4) – floor (N / 128) |
(4.5) |
Поскольку 128 кратно 4, то при значениях N кратных 128 аргументы во втором и третьем слагаемых результирующей части (4.5) будут целочисленными и операторы «floor» можно заменить их аргументами, а смещения моментов завершения 128-летних циклов, представить соотношением:
| Δt (Nкр128 ) = Nкр128• (K – T) + Nкр128 / 4 – Nкр128 / 128 = Nкр128• (K – T + 1 / 4 – 1 / 128) = Nкр128• (K – T + 31 / 128) |
(4.6) |
Найдём для второго приближения максимальное значение Nкр128 , удовлетворяющее критерию корректировки (3.1):
| Nкр128 max • | K – T + 31 / 128 | = 1 сут |
| Nкр128= floor (1 сут / | K – T + 31 / 128 |) |
Подставив численные значения, получим:
| Nкр128= floor (1 сут / | 365 – 365,2422 + 31 / 128 |) = floor 80000 = 80000 |
Из (4.6) устанавливаем, что Δt (Nкр128 ) отрицательны, откуда следует, что продолжительность каждого 80-тысячного КГ должна быть увеличена на 1 сут, т. е. каждый 80-тысячный КГ должен быть високосным, несмотря на то, что значение 80000 кратно 128 и в соответствии со вторым приближением он должен был бы быть простым.
Аргумент оператора «floor» в последнем соотношении оказался целочисленным, откуда вроде бы следует, что третье приближение приводит к «абсолютно» точной структуре календаря, не требующей дальнейших корректировок. Но – это случайность, обусловленная тем обстоятельством, что значение T, полученное из (2.1), было округлено до четвёртого знака. Если принять более точное значение T, то аргумент оператора «floor» целочисленным не будет и теоретически процесс дальнейших приближений мог бы быть продолжен. С другой стороны очевидно, что с практической точки зрения точность, достигнутая вторым приближением, более чем достаточна: просуществует ли вообще человечество 80 тыс. лет – хотя бы до первой корректировки третьим приближением? Поэтому, лишь для полноты картины запишем результирующие соотношения, определяющие моменты завершения любых КГ от начала УЭ и временны́е смещения этих моментов по отношению к моментам завершения соответствующих ТГ с учётом третьего приближения:
| t (NКГ) = N • K + floor (N / 4) – floor (N / 128) + floor (N / 80000) |
(4.7) |
| Δt (N) = N • (K – T) + floor (N / 4) – floor (N / 128) + floor (N / 80000) |
(4.8) |
5. Структура григорианского календаря ↑
Но история пошла другим путём. Не только третье, но и второе приближения в рассмотренном виде приняты не были. Как уже отмечалось, можно подобрать и другие структурные схемы, которые с той или иной степенью точности будут синхронизировать календарные даты с естественными реперными моментами. Исторически сложилось так, что в дополнение к первому, юлианскому, приближению были приняты два других приближения не самые оптимальные с точки зрения сформулированного правила корректировки, но вполне приемлемые для практического применения.
Эти приближения были утверждены в 1582 г. н. э. римским папой Григорием XIII, после чего календарь получил наименование григорианского. Дело в том, что в 325 г. н. э. на Никейском соборе церковь приняла правило, в соответствии с которым праздник Пасхи был привязан ко дню весеннего равноденствия, который в тот год приходился на 21 марта. Но в результате набегающей ошибки ЮК (0,0312 сут за каждые 4 КГ) календарная дата 21 марта постепенно перемещалась на более позднее время по отношению к моменту весеннего равноденствия. А на момент весеннего равноденствия перемещались всё более ранние календарные даты. К 1582 г. н. э., по прошествии 1257 КГ после Никейского собора, в соответствии с (4.2) это смещение достигло почти 10 сут, а на момент весеннего равноденствия переместилась дата 11 марта:
| Δt (1257) = 1257 • (365 – 365,2422) + floor (1257 / 4) = 9,5546 сут ≈ 10 сут |
И для того, чтобы восстановить празднование Пасхи в соответствии с правилами Никейского собора и исключить в дальнейшем их нарушение, реформа содержала два пункта, смысл которых сводился к следующему:
1) дату, наступающую непосредственно после 4 октября 1582 г., считать не 5 октября, а 15 октября;
2) в дальнейшем годы, завершающие столетия, не считать високосными кроме годов, номера которых без остатка делятся на 400.
Первый пункт компенсировал накопившуюся ошибку в 10 сут и в следующем КГ возвращал дату 21 марта на момент весеннего равноденствия.
Вторым пунктом юлианское приближение дополнялось сразу двумя последующими приближениями – вторым и третьим. Действительно, юлианское приближение предписывало считать високосными все КГ кратные 4. Но все КГ, завершающие столетия, кратны 100, а 100 кратно 4. Значит по юлианскому правилу все КГ, завершающие столетия, должны были быть високосными. Но григорианское правило в общем случае исключило КГ, завершающие столетия, из числа високосных. Это можно рассматривать как второе приближение, уточняющее непосредственно юлианское правило. Но вместе с тем, некоторые КГ, завершающие столетия, номера которых кратны 400, григорианское правило всё же предписало считать високосными. Это предписание можно рассматривать как третье приближение, уточняющее два первых.
Запишем соотношение для моментов завершения любых КГ, включающее в себя все три приближения (юлианское и оба григорианских), применительно к УЭ аналогичное соотношениям (4.1), (4.4), (4.7) и рассмотрим его составляющие:
| t (NКГ) = N • K + floor (N / 4) – floor (N / 100) + floor (N / 400) |
(5.1) |
Здесь первые два слагаемых в правой части – повтор соотношения (4.1), описывающего моменты завершения юлианских КГ. Третье слагаемое уменьшает значение t (NКГ) григорианского календаря по сравнению со значением t (NКГ) юлианского календаря на 1 сут за каждые 100 КГ, а четвёртое слагаемое вновь его увеличивает на 1 сут, но уже за каждые 400 КГ. Циклом григорианского календаря следует считать значение 400 КГ.
Используя правило корректировки, найдём для григорианского календаря максимальное значение N, удовлетворяющее критерию корректировки (3.1). Для этого как обычно определим смещения моментов завершения вначале любых григорианских КГ относительно моментов завершения ТГ
| Δt (N) = N • (K – T) + floor (N / 4) – floor (N / 100) + floor (N / 400) |
(5.2) |
а затем, учитывая, что значение N для КГ, завершающих четырёхсотлетние григорианские циклы, кратно знаменателям аргументов всех операторов «floor», запишем значения смещений моментов завершения четырёхсотлетних григорианских циклов:
| Δt (Nкр400 ) = Nкр400• (K – T) + Nкр400 / 4 – Nкр400 / 100 + Nкр400 / 400 = |
|
| = Nкр400• (K – T + 1 / 4 – 1 / 100 + 1 / 400) = Nкр400• (K – T + 97 / 400) |
(5.3) |
Подставив результирующую часть (5.3) в (3.2), составим соответствующее уравнение:
| Nкр400 max • | K – T + 97 / 400 | = 1 сут, |
решив которое и применив оператор «floor», получим целочисленное значение Nкр400 , подлежащее корректировке в четвёртом приближении:
| Nкр400= floor (1 сут / | K – T + 97 / 400 |) |
Подставив численные значения, найдём:
| Nкр400= floor (1 сут / | 365 – 365,2422 + 97 / 400 |) ≈ floor 3333,3333 = 3333 |
Из (5.3) устанавливаем, что Δt (Nкр400 ) положительны, поэтому четвёртую корректировку григорианского календаря следует производить сокращением на 1 сут каждого 3333 КГ. Но 3333 КГ не является високосным – его номер не кратен 4. Поэтому надо или вводить некий «низкокосный» КГ, продолжительностью 364 сут, или – уменьшать продолжительность каждого ближайшего високосного КГ, имеющего меньший номер. Таким ближайшим кратным 4 високосным КГ будет каждый 3332 КГ. Можно применить и корректировку продолжительности КГ кратного 400, т. е. – григорианскому циклу. В этом случае, ближайшим годом, подлежащим сокращению на 1 сут, будет 3200 КГ. Но эти рассуждения имеют лишь теоретический смысл. Поскольку сейчас начало 2000-х КГ григорианского календаря, то до первой корректировки четвёртым приближением у человечества в запасе более тысячи лет и решение этого вопроса можно оставить нашим потомкам. Они разберутся продолжительность которого конкретного КГ будет удобно сократить.
Отметим, что григорианская структура существенно менее точна, чем 128-летняя структура, полученная ранее вторым приближением на основе сформулированного правила корректировки. Календарь, основанный на 128-летних циклах, мог бы обеспечить точность в пределах 1 сут в течение 80 тыс. лет, а григорианский – лишь на протяжении немногим более 3 тыс. лет. Но историческая реальность такова, что для сегодняшнего календаря была принята григорианская структура, которая действует по настоящее время и которую будем рассматривать как данность во всех последующих построениях.
С этого места забываем о существовании ТГ и исчисляем промежутки времени только в сутках и в КГ (вскользь ТГ будут упомянуты в разделе 13 при обсуждении возможных календарных реформ). В качестве основной единицы времени выбираем сутки. Продолжительности периодов и значения моментов времени будем выражать в сутках даже без специального указания на единицу измерения. При исчислении времени годами, обязательно будем делать специальную оговорку или указывать единицу измерения времени «год» или «г.», означающую, что время выражено в количестве календарных годов, которые в суточном измерении могут иметь только целочисленную продолжительность: простой – 365 сут, високосный – 366 сут.
6. Сопоставление дат юлианского и григорианского календарей ↑
Поскольку в европейской традиции кроме григорианского календаря (ГК), действующего по настоящее время, наибольшее значение имел календарь, построенный по юлианской структуре и, так же, как и ГК, ведущий счёт лет от условной даты «Рождества Христова» («РХ»), поставим задачу найти соответствия между датами по ГК и по ЮК. Для её решения надо в первую очередь определить привязки календарей друг к другу по какому-то конкретному событию, момент которого отображён по обоим этим календарям.
В качестве такого события-привязки удобнее всего использовать момент официального начала летосчисления по ГК, опираясь на дату григорианской реформы. По юлианскому календарю – это момент завершения суток, имеющих дату 04.10.1582 ЮК, по григорианскому – момент начала суток, имеющих дату 15.10.1582 ГК.
Построим шкалу времени в суточном отображении, используя дату момента привязки по ЮК. Для этого экстраполируем ЮК в прошлое от момента завершения суток 04.10.1582 ЮК до момента начала первых суток первого года ЮК (01.01.0001 ЮК), совместим с этим моментом нулевую отметку шкалы времени и найдём на этой шкале отметку, соответствующую моменту привязки ГК и ЮК, который по ЮК отображается завершением даты 04.10.1582 ЮК.
Момент начала 1582 г. ЮК соответствует моменту завершения 1581 г. ЮК и для юлианской структуры определяется соотношением (4.1):
| tЮК (1581 ЮК) = 1581 • 365 + floor (1581 / 4) = 577065 + 395 = 577460 сут |
От начала 1582 г. ЮК до начала октября прошло полных 9 месяцев: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь. Количество суток, прошедших за эти месяцы, составляет (год простой, февраль – 28 сут):
| 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 = 273 сут |
Добавив это значение к tЮК (1581 ЮК) и приплюсовав ещё четверо суток, прошедших в течение октября, найдём на шкале времени момент tЮК (04.10.1582 ЮК), которым завершается дата 04.10.1582 ЮК:
| tЮК (04.10.1582 ЮК) = 577460 + 273 + 4 = 577737 сут |
Значение tЮК (04.10.1582 ЮК) = 577737 сут представляет собой количество полных суток, прошедших от нулевой отметки шкалы, построенной по ЮК, до завершения даты 04.10.1582 ЮК, т. е. указывает порядковый номер суток этой шкалы, соответствующих дате 04.10.1582 ЮК, рис. 10.
Аналогично экстраполируя в прошлое ГК, построим шкалу времени этого календаря и найдём на ней тот же момент привязки, который на этой шкале отображается началом даты 15.10.1582 ГК или, что то же самое, – моментом завершения даты 14.10.1582 ГК.
Момент начала 1582 г. ГК – это момент завершения 1581 г. ГК. Применительно к григорианской структуре на шкале времени он определяется соотношением (5.1):
| tГК (1581 ГК) = 1581 • 365 + floor (1581 / 4) – floor (1581 / 100) + floor (1581 / 400) = 577065 + 395 – 15 + 3 = 577448 сут |
От момента начала 1582 г. ГК до начала октября прошли те же полных 9 месяцев, включающих в себя те же 273 сут, как и в случае ЮК. Добавив 14 сут, прошедших в течение октября, найдём на шкале времени момент tГК (14.10.1582 ГК), соответствующий началу даты 15.10.1582 г. ГК:
| tГК (14.10.1582 ГК) = 577448 + 273 + 14 = 577735 сут |
Значение tГК (14.10.1582 ГК) отображает количество полных суток, прошедших от нулевой отметки на шкале, построенной по ГК, до начала даты 15.10.1582 ГК. Поэтому дате 15.10.1582 ГК соответствуют сутки, начинающиеся в этот момент и имеющие на шкале ГК следующий порядковый номер 577736.
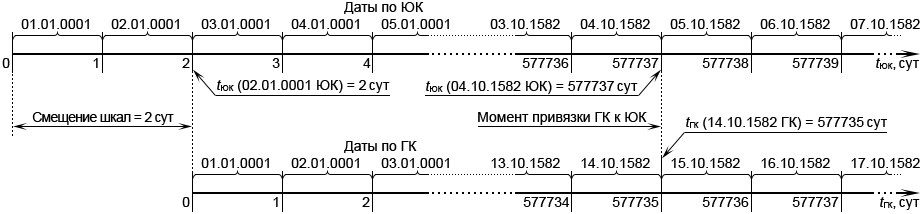
Момент привязки календарей на разных шкалах времени отображается разными значениями: tЮК (04.10.1582 ЮК) = 577737 сут и tГК (14.10.1582 ГК) = 577735 сут. Разница составляет двое суток. Это значит, что при совмещении шкал по моменту привязки их нулевые отметки не совпадут. Первые сутки (01.01.0001 ГК), от начала которых начинается отсчёт времени по шкале ГК, совпадут с третьими сутками (03.01.0001 ЮК) шкалы ЮК (см. рис. 10).
 |
|
Рис. 10. Шка́лы времени ЮК и ГК, совмещённые по моменту привязки
|
Исходя из этого, можно записать простое соотношение связывающее между собой отсчёты времени по шка́лам ЮК и ГК:
где tЮК и tГК – время в сутках, отсчитываемое по соответствующей шкале от её нулевой отметки до какого-либо конкретного события.
Почему появилось такое смещение шкал? Казалось бы, начала отсчётов ЮК и ГК должны совпадать: оба календаря ведут отсчёт от одного и того же события – «РХ». Не имеет значения, является ли это событие реальным или вымышленным. Если оно принято за начало отсчёта, то ему должны соответствовать первые календарные сутки, т. е. и по ЮК, и по ГК – 01.01.0001. А количество суток, прошедших от этого события до другого события (в данном случае, до момента привязки ГК к ЮК), – величина объективная, которая не может зависеть от применённой календарной структуры.
Дело в том, что григорианская реформа проводилась с единственной целью – вернуть на день весеннего равноденствия дату 21 марта, приходившуюся на этот день в год проведения Никейского собора, который в пересчёте на ЮК состоялся в 325 г. ЮК. И поскольку в 1582 г. ЮК на этот день пришлось 11 марта, календарь был скорректирован на величину смещения между этими датами – на 10 сут. Но 10 сут – это смещения дат за 1257 годов, за период лишь от 325 г. ЮК до 1582 г. ЮК. А событие, которому был посвящён праздник Пасхи, произошло (или якобы произошло) на 292 года раньше – в 33 г. ЮК (возраст Иисуса, когда по преданию он был казнён). И за эти 292 года, в силу набегающей ошибки ЮК, датировка дня весеннего равноденствия в соответствии с (4.2) уже сместилась на величину:
| Δt (292) = 292 • (365 – 365,2422) + floor (292 / 4) = 2,2776 сут |
Если в год Никейского собора на день весеннего равноденствия приходилось 21 марта, то в 33 г. ЮК, когда по преданию произошло событие, которому был посвящён праздник Пасхи, на день весеннего равноденствия приходилось 23 марта. Во времена Никейского собора ещё не было известно о набегающей ошибке ЮК. Поэтому его организаторы в принципе не могли учесть это обстоятельство и одновременно с определением правила празднования дня Пасхи ещё и скорректировать календарь таким образом, чтобы на день весеннего равноденствия вернуть 23 марта.
Не учли это обстоятельство и учёные григорианской эпохи, хотя уже выявили некорректность ЮК и на будущее эту некорректность исправили. На день весеннего равноденствия им следовало вернуть не 21 марта, а 23 марта – дату, которая приходилась на этот день в 33 г. ЮК. Если бы они произвели корректировку календаря не на 10 сут, а на 12 сут, то получили бы корректный результат, к которому приводит суммирование значений обоих смещений Δt (1257) = 9,5546 сут (см. начало раздела 5) и Δt (292) = 2,2776 сут:
| 9,5546 + 2,2776 = 11,8322 сут ≈ 12 сут |
В этом случае, нулевые отметки шкал по ЮК и по ГК совпали бы между собой. Хотя, если говорить строго, то корректировать календарь следовало именно по нулевым отметкам – не по событию, приуроченному к Пасхе, а по событию, приуроченному к Рождеству, поскольку именно от него уже велось летосчисление 8. Но учитывая, что между Рождеством и Пасхой прошло всего 33 г., и за этот период ни один из столетних рубежей, которые и привносят расхождение между датировками по ЮК и по ГК, не был пройден, это обстоятельство особого значения не имело. Вычисление смещения дат от начала летосчисления до начала 1582 г. ЮК (соответствует моменту завершения 1581 г. ЮК) при округлении приводит к тому же результату:
| Δt (1581) = 1581 • (365 – 365,2422) + floor (1581 / 4) = 12,0818 сут ≈ 12 сут |
Итак, календарь, которым мы пользуемся сегодня и называем григорианским, был скорректирован со смещением начала отсчёта на двое суток по отношению к календарю, который сегодня мы называем юлианским. Не следует строго судить за эту ошибку учёных григорианской эпохи. Дело в том, что и 1 г. н. э. от «РХ», и 33 г. н. э. от «РХ», и 325 г. н. э. от «РХ» получили такие номера лишь после того, как был изобретён счёт лет от «РХ». А произошло это в VI в. н. э. До этого счёт лет вёлся по другим календарным системам. Учёным XVI в. н. э. в расчётах приходилось пользоваться календарями, которые почти за тысячу лет до проводимой реформы уже прекратили существование. Запутаться в них и упустить какие-то детали было очень просто. Кроме того не могло не сыграть роль и то обстоятельство, что Рождество и Пасха приурочены к мифическим событиям, реальные даты которых хотя бы по какому-то календарю вообще не известны.
Записывать в аналитической форме соотношения, непосредственно переводящие даты ЮК в даты ГК и наоборот нецелесообразно. Они громоздки и неудобны. Фактически, для каждого месяца надо создавать отдельное соотношение, да ещё и с учётом простого или високосного года. Это связано с тем, что месяцы имеют различную продолжительность, чередование которой бессистемно, а продолжительность февраля ещё и непостоянна. Для перевода датировок между ЮК и ГК можно создать таблицы, принцип построения которых достаточно прост: в годы, номера которых кратны 100, но не кратны 400, после даты 29 фев. ЮК (которая в эти годы отсутствует в ГК) смещения между всеми последующими датами ЮК и ГК в этом и во всех последующих годах должны быть увеличены на одни сутки по сравнению с предшествующим годом.
С появлением ЭВМ таблицы стали заменяться простыми программами. Одна из таких программ предлагается и в настоящей статье (раздел 12). Но прежде, чем обратиться к программным расчётам, рассмотрим ещё некоторые моменты и, в частности, календарь от «Сотворения Мира», который появился задолго до изобретения счёта лет от «РХ» и на который в т. ч. скорее всего опирались учёные при подготовке григорианской реформы.
7. Летосчисление от «Сотворения Мира» ↑
До изобретения счёта лет от «РХ» в европейской традиции летосчисление велось от ещё более мифического события – от «Сотворения Мира» («СМ»). Различных систем счёта лет от «СМ» было несколько. Остановимся на византийской, которая вместе с православием была привнесена в Россию в X в. н. э. Россия придерживалась этого, почти в прямом смысле «допотопного», византийского календаря (ВК) около восьми веков. Особенностью ВК было ещё и то обстоятельство, что начало года было приурочено к 01 сент., вместо 01 янв., как это практиковалось в европейской традиции. Лишь Пётр I указом от 19 дек. 7208 ВК повелел вместо 01 янв. 7208 ВК считать 01 янв. 1700 ЮК и впредь исчислять начало года с 01 янв. Этот указ даёт возможность привязать даты ВК к датам ЮК.
Построим две шкалы времени, опираясь на момент этой привязки, аналогично тому, как это было сделано в разделе 6 для привязки дат ГК к датам ЮК. Поскольку в ВК первым месяцем года является сентябрь, то, во избежание путаницы, в дальнейшем месяцы в датировках по ВК будем обозначать только их названиями, но не номерами. Иначе, в силу привычки, даты, например, 19.04.7208 ВК или 01.05.7208 ВК могут быть приняты за 19 апр. и 01 мая. 7208 ВК, хотя по ВК – это 19 дек. и 01 янв. 7208 ВК.
На шкале ЮК момент привязки отобразить просто. Момент начала 1700 ЮК – это момент завершения 1699 ЮК. Находим его используя (4.1):
| tЮК (1699 ЮК) = 1699 • 365 + floor (1699 / 4) = 620135 +floor 424,75 = 620135 + 424 = 620559 сут |
Поскольку момент привязки совпадает с началом первых суток 1700 г. ЮК, то добавлять дополнительные месяцы или дополнительные сутки не требуется, и отметка на шкале времени, обозначающая момент завершения даты 31.12.1699 ЮК, совпадающая с началом даты 01.01.1700 ЮК, определится значением tЮК (1699 ЮК):
| tЮК (31.12.1699 ЮК) = t (1699 ЮК) = 620559 сут, |
а дате 01.01.1700 ЮК на шкале ЮК будут соответствовать сутки, имеющие следующий порядковый номер 620560 сут.
Построим шкалу ВК. ВК тоже был построен по юлианской структуре, поэтому все соотношения раздела 4 для ЮК в полной мере применимы и к ВК. Момент начала 7208 г. ВК – это момент завершения 7207 г. ВК и, в соответствии с (4.1),
| tВК (7207 ВК) = 7207 • 365 + floor (7207 / 4) = 2630555 +floor 1801,75 = 2630555 + 1801 = 2632356 сут |
Но 7208 г. ВК начинается с 01 сент. До момента привязки, т. е. до начала даты 01 янв. 7208 ВК, прошло ещё четыре полных месяца: сентябрь, октябрь, ноябрь, декабрь, сумма суток в которых составляет:
| 30 + 31 + 30 + 31 = 122 сут |
И на шкале времени ВК момент привязки, соответствующий моменту завершения даты 31 дек. 7208 ВК, отобразится суммой:
| tВК (31 дек. 7208 ВК) = t (7207 ВК) + 122 = 2632356 + 122 = 2632478 сут |
Разность значений tВК (31 дек. 7208 ВК) и tЮК (31.12.1699 ЮК) определит смещение шкалы ЮК относительно шкалы ВК:
| tВК (31 дек. 7208 ВК) – tЮК (31.12.1699 ЮК) = 2632478 – 620559 = 2011919 сут |
Нулевая отметка шкалы ЮК отобразится на шкале ВК моментом tВК (31 дек. 5509 ВК) = 2011919 сут. Это значение можно представить как сумму двух периодов: количества суток, прошедших от нулевой отметки ВК до завершения 5508 г. ВК, плюс количество суток, прошедших от начала 5509 г. ВК (от начала даты 01 сен. 5509 ВК) до завершения даты 31 дек. 5509 ВК. Первое слагаемое определяется соотношением (4.1) для N = 5508, а второе – 122 сут, прошедших за первые четыре месяца (сентябрь, октябрь, ноябрь, декабрь) 5509 г. ВК:
| tВК (5508 ВК) = 5508 • K + floor (5508 / 4) = 5508 • 365 + floor (1377) = 2010420 + 1377 = 2011797 сут |
| tВК (31 дек. 5509 ВК) = t (5508 ВК) + 122 = 2011797 + 122 = 2011919 сут |
Сутки, датируемые по ЮК как 01.01.0001 ЮК, по ВК датируются как 01 янв. 5509 ВК.
Аналогично 6.1 запишем соотношение связывающее между собой отсчёты времени по шкалам ВК и ЮК:
| tЮК = tВК – 2011919 |
(7.1) |
где tВК и tЮК – время в сутках, отсчитываемое по соответствующей шкале от её нулевой отметки до какого-либо конкретного события.
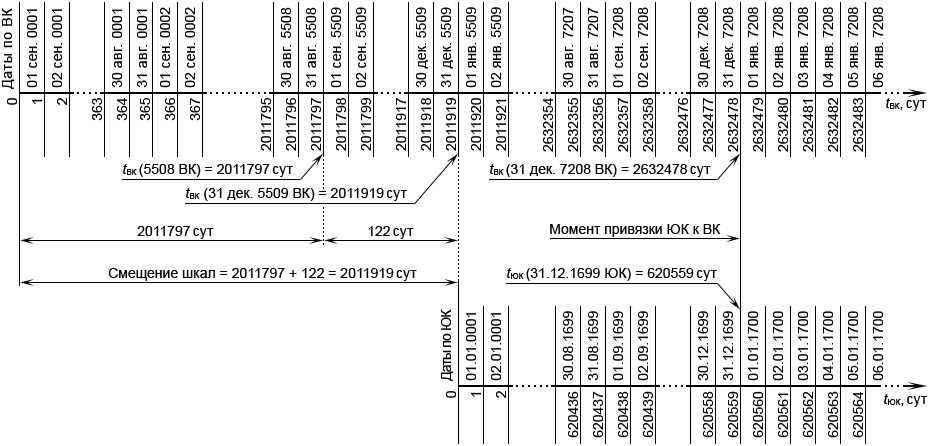
Изложенное проиллюстрировано на рис. 11.
 |
|
Рис. 11. Шка́лы времени ВК и ЮК, совмещённые по моменту привязки
|
Вкратце отметим, что сказанное относится к ВК «сентябрьского стиля». В раннехристианской Руси наряду с ВК сентябрьского стиля применялись ещё два стиля: «мартовский» и «ультрамартовский». Их отличие от сентябрьского заключалось в том, что начало года было приурочено не к 01 сентября, а к какому-либо из чисел марта. Причём порой эти числа выбирались достаточно произвольно. Мартовский стиль смещал номера годов сентябрьского ВК на пол года на более позднюю дату, а ультрамартовский – на пол года на более раннюю. Месяцы и собственно даты внутри месяцев сохранялись теми же, что и в ВК сентябрьского стиля. После 7000 г. ВК (1492 г. ЮК) Иван III отменил применение мартовских стилей, оставив только сентябрьский. Далее будем рассматривать ВК только сентябрьского стиля.
8. Упрощённые датировки и выбор основной шкалы времени ↑
Изменим обозначения датировок внутри года следующим образом. Пронумеруем все сутки года номерами в порядке возрастания. В простом году первым суткам присвоим номер 001, вторым суткам – номер 002 и т. д. до последних суток года, которые будут иметь номер 365. Поскольку високосный год содержит на одни сутки больше, то его последние сутки должны иметь номер 366. Но удобнее оставить последним суткам високосного года номер 365, а дополнительные сутки вставить в начало года, присвоив им номер 000. Номера суток, количество цифр в которых менее трёх, всегда будем дополнять незначащими нулями до трёх знаков, а номера годов, содержащие менее четырёх знаков, – незначащими нулями до четырёх знаков. Теперь любые сутки любого года можно отобразить двумя числами – трёхзначным номером суток внутри года и четырёхзначным номером года, которому они принадлежат, разделив их между собой точкой (или косой чертой, дефисом): ddd.yyyy, где yyyy – номер года по рассматриваемому календарю, а ddd – порядковый номер суток внутри этого года, не превышающий 365. Назовём такие даты «упрощёнными». При необходимости, индексом упрощённой датировки будем указывать тип календаря, по которому она произведена. Такая система обозначений позволит составить соотношения пересчёта дат одного календаря в даты другого календаря без обращения к месяцу, который по сути является лишней переменной и запутывает пересчёт. Значения ddd всегда будут иметь размерность суток (сут), а значения yyyy – всегда размерность годов (г.).
 |
|
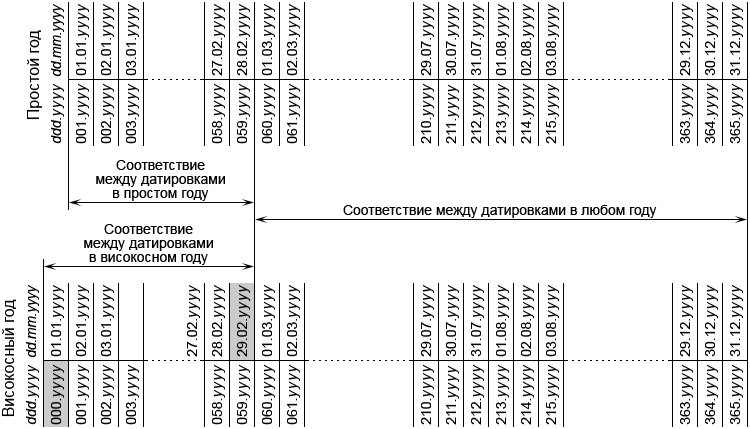
Рис. 12. Соответствие между обычными и упрощёнными датировками для ЮК и ГК
«dd.mm.yyyy» – обычные даты; «ddd.yyyy» – упрощённые даты.
Дополнительные сутки високосного года – 29.02.yyyy и 000.yyyy – выделены затемнённым фоном.
|
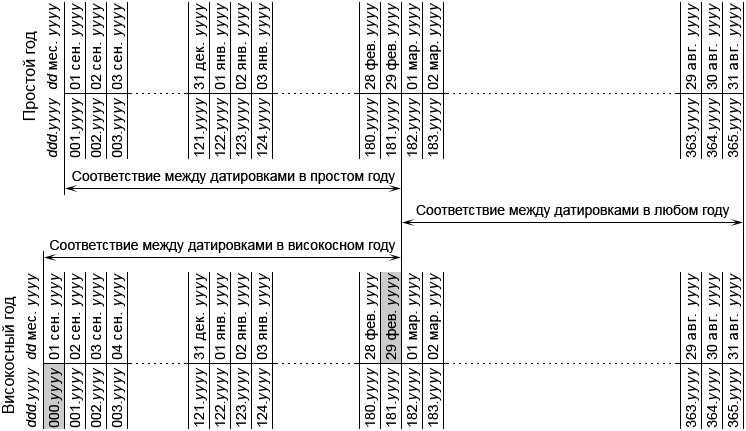
Рис. 12 поясняет суть введённого упрощения для ЮК и ГК, а рис. 13 – для ВК. Для ЮК и ГК соответствие между обычными и упрощёнными датами в простых и високосных годах различаются только для двух первых месяцев – января и февраля. Для остальных 10 месяцев с марта по декабрь соответствия между датами не зависят от типа года. Если бы дополнительный день високосного года в упрощённой датировке был обозначен не номером 000, а номером 366 и вставлен в конец года, то ситуация была бы обратной. Поскольку в календаре ВК год начинается с 01 сентября, то для ВК соответствие между обычными и упрощёнными датировками в простых и високосных годах различаются для первых шести месяцев – с сентября по февраль. А соответствия между датировками, не зависящие от типа года, сохраняются только для оставшихся шести месяцев с марта по август. Таким образом, для ВК безразлично в начало или в конец високосного года вставить дополнительные сутки. Но для единообразия с ГК и ЮК дополнительные сутки високосного года тоже вставлены в его начало под номером 000.
 |
|
Рис. 13. Соответствие между обычными и упрощёнными датировками для ВК
«dd мес.yyyy» – обычные даты; «ddd.yyyy» – упрощённые даты.
Дополнительные сутки високосного года – 29 фев.yyyy и 000.yyyy – выделены затемнённым фоном.
|
Соотношения, связывающие обычные даты ЮК и ГК с упрощёнными датами ЮК и ГК, представлены в табл. 4, а соотношения, связывающие обычные даты ВК с упрощёнными датами ВК, – в табл. 5. Здесь dd – номера суток внутри месяцев обычных дат, ddd – номера суток внутри года упрощённых дат. Каждое соотношение применимо лишь в интервале номеров суток обычных дат dd конкретного месяца, указанного в первой (левой) колонке, и в соответствующих интервалах номеров суток упрощённых дат ddd, указанных в последней (правой) колонке.
| Табл. 4 |
Связь упрощённых дат ddd с обычными датами dd для ЮК и ГК;
v = 0 для простого года; v = 1 для високосного года |
| Мес. |
dd – обычная дата,
ddd – упрощённая дата |
Допустимый интервал
значений ddd |
| 01 |
ddd = dd – v |
dd = ddd + v |
(1–v ) ≤ ddd ≤ (31–v ) |
| 02 |
ddd = dd+31–v |
dd = ddd – 31+v |
(32 – v ) ≤ ddd ≤ 59 |
| 03 |
ddd = dd + 59 |
dd = ddd – 59 |
60 ≤ ddd ≤ 90 |
| 04 |
ddd = dd + 90 |
dd = ddd – 90 |
91 ≤ ddd ≤ 120 |
| 05 |
ddd = dd + 120 |
dd = ddd – 120 |
121 ≤ ddd ≤ 151 |
| 06 |
ddd = dd + 151 |
dd = ddd – 151 |
152 ≤ ddd ≤ 181 |
| 07 |
ddd = dd + 181 |
dd = ddd – 181 |
182 ≤ ddd ≤ 212 |
| 08 |
ddd = dd + 212 |
dd = ddd – 212 |
213 ≤ ddd ≤ 243 |
| 09 |
ddd = dd + 243 |
dd = ddd – 243 |
244 ≤ ddd ≤ 273 |
| 10 |
ddd = dd + 273 |
dd = ddd – 273 |
274 ≤ ddd ≤ 304 |
| 11 |
ddd = dd + 304 |
dd = ddd – 304 |
305 ≤ ddd ≤ 334 |
| 12 |
ddd = dd + 334 |
dd = ddd – 334 |
335 ≤ ddd ≤ 365 |
|
|
|
|
| Табл. 5 |
Связь упрощённых дат ddd с обычными датами dd для ВК;
v = 0 для простого года; v = 1 для високосного года |
| Мес. |
dd – обычная дата,
ddd – упрощённая дата |
Допустимый интервал
значений ddd |
| сен. |
ddd = dd – v |
dd = ddd + v |
(1–v ) ≤ ddd ≤ (30–v ) |
| окт. |
ddd = dd+30–v |
dd = ddd – 30+v |
(31–v ) ≤ ddd ≤ (61–v ) |
| ноя. |
ddd = dd+61–v |
dd = ddd – 61+v |
(62–v ) ≤ ddd ≤ (91–v ) |
| дек. |
ddd = dd+91–v |
dd = ddd – 91+v |
(92–v ) ≤ ddd ≤ (122–v ) |
| янв. |
ddd = dd+122–v |
dd = ddd – 122+v |
(123–v ) ≤ ddd ≤ (153–v ) |
| фев. |
ddd = dd+153–v |
dd = ddd – 153+v |
(154 – v ) ≤ ddd ≤ 181 |
| март |
ddd = dd + 181 |
dd = ddd – 181 |
182 ≤ ddd ≤ 212 |
| апр. |
ddd = dd + 212 |
dd = ddd – 212 |
213 ≤ ddd ≤ 243 |
| май |
ddd = dd + 243 |
dd = ddd – 243 |
244 ≤ ddd ≤ 273 |
| июнь |
ddd = dd + 273 |
dd = ddd – 273 |
274 ≤ ddd ≤ 304 |
| июль |
ddd = dd + 304 |
dd = ddd – 304 |
305 ≤ ddd ≤ 334 |
| авг. |
ddd = dd + 334 |
dd = ddd – 334 |
335 ≤ ddd ≤ 365 |
|
|
|
|
| |
|
Параметр v корректирует соотношения и интервалы в зависимости от типа года: для простого года v = 0, для високосного года v = 1. Значение параметра v легко представить аналитически используя в дополнение к оператору «floor» другой оператор, применяемый в программировании, – оператор «ceil», который тоже производит округление аргумента, но, в противовес оператору «floor», до ближайшего целого числа в бо́льшую сторону.
Для ЮК и ВК, имеющих юлианскую структуру, значения vЮК (yyyyЮК) и vВК (yyyyВК) найдём из соотношений:
| vЮК (yyyyЮК) = 1 – ceil [yyyyЮК / 4 – floor (yyyyЮК / 4)] |
(8.1) |
| vВК (yyyyВК) = 1 – ceil [yyyyВК / 4 – floor (yyyyВК / 4)] |
(8.2) |
Для ГК значение vГК (yyyyГК) найдём из соотношения:
| vГК (yyyyГК) = 1 – ceil [yyyyГК / 4 – floor (yyyyГК / 4)] + ceil [yyyyГК / 100 – floor (yyyyГК / 100)] – ceil [yyyyГК / 400 – floor (yyyyГК / 400)] |
(8.3) |
При переходе от обычных дат к упрощённым и наоборот номер года yyyy остаётся прежним, а структура соотношений зависит не от номера года, а только от его типа – простой или високосный. Поэтому соответствия между обычными и упрощёнными датами можно вычислить для всего массива дат простых и високосных годов, а результаты свести в таблицы, которые можно использовать вместо соотношений из табл. 4, 5 вне зависимости от номера года учитывая только его тип. Такие таблицы приведены в Приложении.
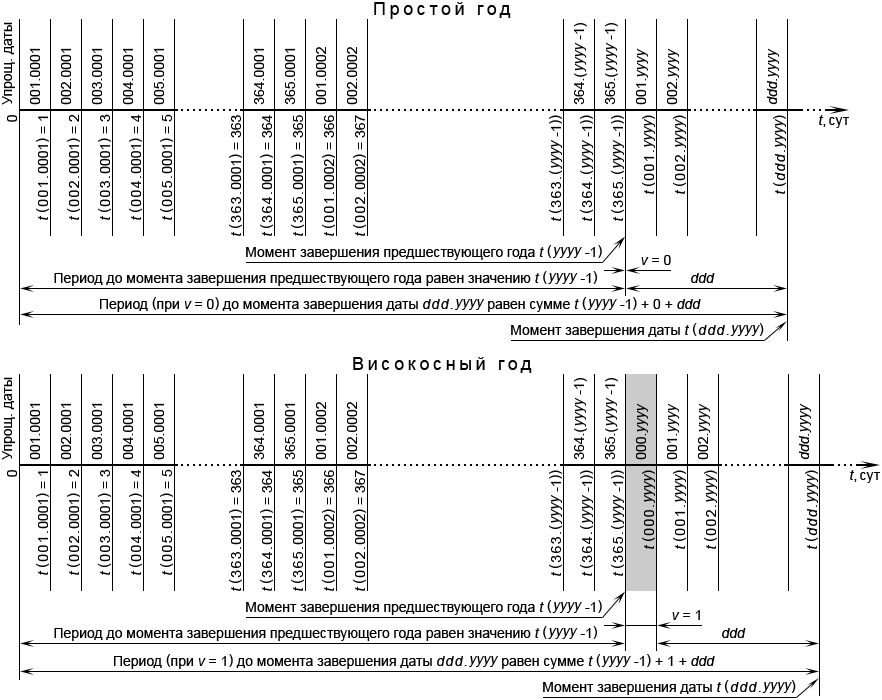
Переведя обычную дату в упрощённую, момент её завершения можно отобразить на шкале времени своего календаря, рис. 14. Значение этого момента может быть отображено суммой трёх слагаемых:
- периодом, прошедшим от нулевого момента шкалы до момента завершения предшествующего года;
- корректирующим параметром v (yyyy), зависящим от типа года и смещающим все даты високосного года на единицу;
- порядковым номером ddd упрощённой даты внутри года yyyy :
| t (ddd.yyyy) = t (yyyy – 1) + v (yyyy) + ddd |
(8.4) |
где: t (ddd.yyyy) – момент завершения даты ddd.yyyy на шкале времени своего календаря;
t (yyyy – 1) – момент завершения предшествующего года на шкале времени своего календаря;
v (yyyy) – корректирующий параметр: v = 0 для простого года, v = 1 для високосного года;
ddd – порядковый номер суток внутри года, имеющего номер yyyy.
 |
|
Рис. 14. Схема, поясняющая структуру соотношения (8.4)
|
Для ЮК и ВК, имеющих юлианскую структуру, момент завершения предшествующего года t (yyyy – 1) на своих шкалах найдём из (4.1) при N = (yyyy – 1) и K = 365. Для этих календарей соотношение (8.4) перепишем в виде:
| tЮК (ddd.yyyyЮК) = 365 • (yyyyЮК – 1) + floor [(yyyyЮК – 1) / 4] + vЮК (yyyyЮК) + dddЮК |
(8.5) |
| tВК (ddd.yyyyВК) = 365 • (yyyyВК – 1) + floor [(yyyyВК – 1) / 4] + vВК (yyyyВК) + dddВК |
(8.6) |
Для ГК момент завершения предшествующего года t (yyyy – 1) найдём из (5.1) при аналогичных значениях N = (yyyy – 1) и K = 365, а соотношение (8.4) перепишем в виде:
| tГК (ddd.yyyyГК) = 365 • (yyyyГК – 1) + floor [(yyyyГК – 1) / 4] – floor [(yyyyГК – 1) / 100] + floor [(yyyyГК – 1) / 400] + vГК (yyyyГК) + dddГК |
(8.7) |
С помощью соотношений (8.5) – (8.7), предварительно преобразовав обычную дату любого календаря в упрощённую, момент её завершения можно отобразить на шкале времени своего календаря.
Какую-либо из шкал удобно выбрать в качестве основной, и отсчёты времени по всем шкалам приводить к значениям t этой основной шкалы. Исторически сложилось так, что нулевая отметка шкалы ЮК была выбрана в качестве начала эры, получившей название «Наша эра» или «Новая эра». Все даты, начиная с 01.01.0001 ЮК и далее в сторону возрастания, считаются датами Нашей эры, а все более ранние даты – датами до Нашей эры 9. Исходя из этой исторической предпосылки, в качестве основной шкалы целесообразно выбрать шкалу, совпадающую со шкалой ЮК. В этом случае, значение t = 0 основной шкалы будет соответствовать моменту начала Нашей эры, все положительные значения t – относиться к Нашей эре, а все отрицательные значения t – к периоду до Нашей эры, рис. 15.
 |
|
Рис. 15. Основная шкала времени и её связь со шкалами ЮК, ГК, ВК
|
Время, отображаемое на основной шкале, будем обозначать символом t без индекса, указывающего тип календаря. Учитывая (6.1) и (7.1), запишем соотношения, связывающие шкалы времени каждого из трёх календарей с основной шкалой:
| t = tЮК |
(8.8) |
| t = tВК – 2011919 |
(8.9) |
| t = tГК + 2 |
(8.10) |
Подставив сюда значения tЮК, tВК, tГК из (8.5) – (8.7), получим соотношения, позволяющие отобразить момент завершения любой упрощённой даты ddd.yyyy любого календаря моментом на основной шкале времени.
Для ЮК момент завершения даты ddd.yyyyЮК отобразится на основной шкале времени значением:
| t = 365 • (yyyyЮК – 1) + floor [(yyyyЮК – 1) / 4] + vЮК (yyyyЮК) + dddЮК |
(8.11) |
Для ВК момент завершения даты ddd.yyyyВК – значением:
| t = 365 • (yyyyВК – 1) + floor [(yyyyВК – 1) / 4] + vВК (yyyyВК) + dddВК – 2011919 |
(8.12) |
Для ГК момент завершения даты ddd.yyyyГК – значением:
| t = 365 • (yyyyГК – 1) + floor [(yyyyГК – 1) / 4] – floor [(yyyyГК – 1) / 100] + floor [(yyyyГК – 1) / 400] + vГК (yyyyГК) + dddГК + 2 |
(8.13) |
Значения vЮК (yyyyЮК), vВК (yyyyВК), vГК (yyyyГК) находятся из (8.1) – (8.3) для соответствующих значений yyyyЮК , yyyyВК , yyyyГК .
Таким образом, переведя обычную дату любого календаря в упрощённую по соотношениям из табл. 4, 5 (или по таблицам Приложения) и воспользовавшись соотношениями (8.11) – (8.13), момент t её завершения можно отобразить на основной шкале времени. Найденное значение t будет соответствовать порядковому номеру суток, завершающихся в этот момент и отсчитываемых от нулевой отметки t = 0 основной шкалы времени.
9. Обратные преобразования значений t основной шкалы в даты ЮК, ВК, ГК ↑
Рассмотрим обратную задачу – преобразование значений t основной шкалы времени в даты конкретных календарей. Поскольку значения t основной шкалы по соотношениям (8.8) – (8.10) легко переводятся в значения отсчётов времени по шкалам своих календарей, то решение задачи сводится к преобразованию в даты отсчётов значений времени своих шкал для каждого календаря. Начнём с ЮК.
Для любого календаря упрощённая дата связана со значением момента времени на своей шкале соотношением (8.4). Перепишем его применительно к ЮК, выразив номер суток dddЮК , принадлежащих году yyyyЮК , через остальные составляющие:
| dddЮК = tЮК (ddd.yyyyЮК) – tЮК (yyyyЮК – 1) – vЮК (yyyyЮК) |
(9.1) |
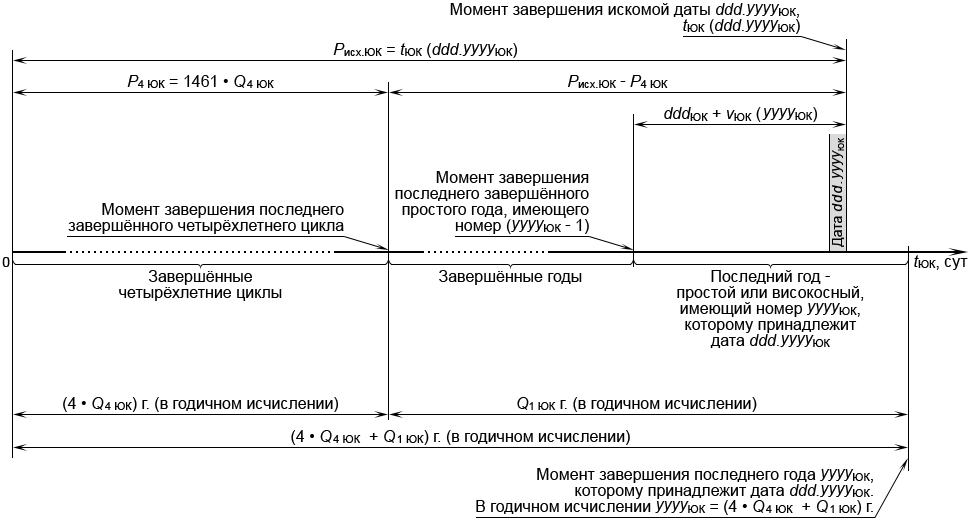
Первый член tЮК (ddd.yyyyЮК) правой части (9.1) представляет собой момент завершения искомой даты ddd.yyyyЮК численно равный периоду времени, прошедшего от начала шкалы tЮК = 0 до завершения этой даты, рис. 16:
| Pисх.ЮК = tЮК (ddd.yyyyЮК) |
(9.2) |
Для того, чтобы определить второй и третий члены правой части (9.1), требуется найти номер yyyyЮК года, которому принадлежит дата ddd.yyyyЮК .
 |
|
Рис. 16. Схема, поясняющая процесс создания алгоритма преобразования t в ddd.yyyyЮК
|
ЮК состоит из периодически повторяющихся одинаковых четырёхлетних циклов продолжительностью 1461 сут (раздел 2). Это значение легко получить и из соотношения (4.1) при N = 4:
| tЮК (4) = 4 • 365 + floor (4 / 4) = 1461 |
Используя оператор «floor» и учитывая (9.2), найдём количество Q4 ЮК завершённых четырёхлетних циклов, прошедших за период Pисх.ЮК от нулевого момента tЮК = 0 до завершения даты ddd.yyyyЮК :
| Q4 ЮК = floor (Pисх.ЮК / 1461) = floor [tЮК (ddd.yyyyЮК) / 1461] |
(9.3) |
Умножив продолжительность 1461 сут четырёхлетнего цикла на Q4 ЮК , найдём период времени P4 ЮК , занятый всеми завершёнными четырёхлетними циклами, прошедшими до завершения даты ddd.yyyyЮК :
| P4 ЮК = 1461 • Q4 ЮК |
(9.4) |
Период времени (Pисх.ЮК – P4 ЮК) от момента завершения последнего завершённого четырёхлетнего цикла до момента завершения года, которому принадлежит дата ddd.yyyyЮК , может состоять не более чем из трёх простых завершённых годов и последнего простого или високосного года. Используя оператор «ceil» (округление вверх) и учитывая (9.2) и (9.4), найдём количество Q1 ЮК годов, прошедших от момента завершения периода P4 ЮК до момента завершения года yyyyЮК , включающего дату ddd.yyyyЮК :
| Q1 ЮК = ceil [(Pисх.ЮК – P4 ЮК) / 365] = ceil [(tЮК (ddd.yyyyЮК) – 1461 • Q4 ЮК) / 365] |
(9.5) |
Сумма годов, прошедших от момента tЮК = 0 до момента завершения этого года, укажет его номер. Поскольку в годичном исчислении продолжительность периода P4 ЮК составляет (4 • Q4 ЮК) г., этот номер отобразится соотношением:
| yyyyЮК = (4 • Q4 ЮК + Q1 ЮК) г. |
(9.6) |
Выражение для второго члена tЮК (yyyyЮК – 1) правой части (9.1) найдём из (4.1) при N = (yyyyЮК – 1) и K = 365:
| tЮК (yyyyЮК – 1) = 365 • (yyyyЮК – 1) + floor [(yyyyЮК – 1) / 4] |
(9.7) |
Подставив (9.7) в правую часть (9.1), найдём соотношение для вычисления номера суток dddЮК внутри года yyyyЮК :
| dddЮК = tЮК (ddd.yyyyЮК) – {365 • (yyyyЮК – 1) + floor [(yyyyЮК – 1) / 4]} – vЮК (yyyyЮК) = |
|
| = tЮК (ddd.yyyyЮК) – 365 • (yyyyЮК – 1) – floor [(yyyyЮК – 1) / 4] – vЮК (yyyyЮК) |
(9.8) |
На основании (9.3), (9.5), (9.6), (8.1) и (9.8) с учётом (8.8) запишем алгоритм вычисления составляющих упрощённой даты ЮК по значению t основной шкалы:
| Табл. 6 |
Алгоритм преобразования значений t основной шкалы
в упрощённые даты ЮК |
| 1. |
Q4 ЮК= floor (t / 1461) |
| 2. |
Q1 ЮК= ceil [(t – 1461 • Q4 ЮК) / 365] |
| 3. |
yyyyЮК = (4 • Q4 ЮК + Q1 ЮК) г. |
| 4. |
vЮК (yyyyЮК) = 1 – ceil [(yyyyЮК / 4 – floor (yyyyЮК / 4)] |
| 5. |
dddЮК = t – 365 • (yyyyЮК – 1) – floor [(yyyyЮК – 1) / 4] – vЮК (yyyyЮК) |
|
| |
Поскольку ВК имеет такую же юлианскую структуру как ЮК, общие рассуждения относительно ЮК применимы и к ВК. Разница состоит лишь в том, что значение момента tВК (ddd.yyyyВК) завершения даты ddd.yyyyВК , определяющее период Pисх.ВК , находим по исходному значению t из (8.9):
| Pисх.ВК = tВК (ddd.yyyyВК) = t + 2011919 |
(9.9) |
Соотношение (8.4), переписанное применительно к ВК, приобретает вид:
| dddВК = tВК (ddd.yyyyВК) – tВК (yyyyВК – 1) – vВК (yyyyВК) = t – tВК (yyyyВК – 1) – vВК (yyyyВК) + 2011919 |
(9.10) |
Учитывая (9.9), в соотношениях аналогичных (9.3) и (9.5) для вычисления Q4 ВК и Q1 ВК период Pисх.ВК следут заменить суммой (t + 2011919):
| Q4 ВК = floor [(Pисх.ВК) / 1461] = floor [(t + 2011919) / 1461] |
| Q1 ВК = ceil [(Pисх.ВК – P4 ВК) / 365] = ceil [(t – 1461 • Q4 ВК + 2011919) / 365] |
Соотношения, определяющие номер yyyyВК искомого года и второй член tВК (yyyyВК – 1) правой части (9.10), полностью аналогичны таковым для ЮК (см. (9.6), (9.7)) и могут быть получены из них простой заменой индексов «ЮК» на «ВК». Параметр vВК (yyyyВК) находим из (8.2). С учётом этого, алгоритм вычисления упрощённой даты ВК по значению t основной шкалы запишем в виде:
| Табл. 7 |
Алгоритм преобразования значений t основной шкалы
в упрощённые даты ВК |
| 1. |
Q4 ВК = floor [(t + 2011919) / 1461] |
| 2. |
Q1 ВК = ceil [(t – 1461 • Q4 ВК + 2011919) / 365] |
| 3. |
yyyyВК = (4 • Q4 ВК + Q1 ВК) г. |
| 4. |
vВК (yyyyВК) = 1 – ceil [(yyyyВК / 4 – floor (yyyyВК / 4)] |
| 5. |
dddВК = t – 365 • (yyyyВК – 1) – floor [(yyyyВК – 1) / 4] – vВК (yyyyВК) + 2011919 |
|
| |
Применительно к ГК, значение момента tГК (ddd.yyyyГК) завершения даты ddd.yyyyГК , определяющее период Pисх.ГК , по исходному значению t находим из (8.10):
| Pисх.ГК = tГК (ddd.yyyyГК) = t – 2 |
(9.11) |
Соотношение (8.4) для ГК приобретает вид:
| dddГК = tГК (ddd.yyyyГК) – tГК (yyyyГК – 1) – vГК (yyyyГК) = t – tГК (yyyyГК – 1) – vГК (yyyyГК) – 2 |
(9.12) |
ГК формируется тремя приближениями, каждое из которых определяет собственный цикл: 400-летний, 100-летний, 4-летний. Их продолжительности находим из (5.1):
| tГК (400) = 400 • 365 + floor (400 / 4) – floor (400 / 100) + floor (400 / 400) = 146097 |
| tГК (100) = 100 • 365 + floor (100 / 4) – floor (100 / 100) + floor (100 / 400) = 36524 |
| tГК (4) = 4 • 365 + floor (4 / 4) – floor (4 / 100) + floor (4 / 400) = 1461 |
Количество Q400 ГК завершённых 400-летних циклов за период Pисх.ГК от нулевого момента tГК = 0 до завершения даты ddd.yyyyГК и продолжительность периода P400 ГК , занятого всеми завершёнными 400-летними циклами равны:
| Q400 ГК = floor [(Pисх.ГК) / tГК (400)] = floor [(t – 2) / 146097] |
(9.13) |
| P400 ГК = tГК (400) • Q400 ГК = 146097 • Q400 ГК |
|
Количество Q100 ГК завершённых 100-летних циклов (их может быть не более 3-х) за период (Pисх.ГК – P400 ГК) от момента завершения последнего завершённого 400-летнего цикла до момента завершения даты ddd.yyyyГК и продолжительность периода P100 ГК , занятого всеми завершёнными 100-летними циклами, не вошедшими в завершённые 400-летние циклы, равны:
| Q100 ГК = floor [(Pисх.ГК – P400 ГК) / tГК (100)] = floor [(t – 146097 • Q400 ГК – 2) / 36524] |
(9.14) |
| P100 ГК = tГК (100) • Q100 ГК = 36524 • Q100 ГК |
|
Количество Q4 ГК завершённых 4-летних циклов (их может быть не более 24-х) за период (Pисх.ГК – P400 ГК – P100 ГК) от момента завершения последнего завершённого 100-летнего цикла до момента завершения даты ddd.yyyyГК и продолжительность периода P4 ГК , занятого всеми завершёнными 4-летними циклами, не вошедшими в завершённые 400-летние и 100-летние циклы, равны:
| Q4 ГК = floor [(Pисх.ГК – P400 ГК – P100 ГК) / tГК (4)] = floor [(t – 146097 • Q400 ГК – 36524 • Q100 ГК – 2) / 1461] |
(9.15) |
| P4 ГК = tГК (4) • Q4 ГК = 1461 • Q4 ГК |
|
Период времени от момента завершения последнего завершённого четырёхлетнего цикла до момента завершения года, которому принадлежит дата ddd.yyyyГК , может состоять не более чем из трёх простых завершённых годов и последнего простого или високосного года. Используя оператор «ceil», найдём количество Q1 ГК годов, прошедших от момента завершения периода P4 ГК до момента завершения года, включающего дату ddd.yyyyГК :
| Q1 ГК = ceil [(Pисх.ГК – P400 ГК – P100 ГК – P4 ГК) / 365] = ceil [(t – 146097 • Q400 ГК – 36524 • Q100 ГК – 1461 • Q4 ГК – 2) / 365] |
(9.16) |
Номер yyyyГК года, которому принадлежит дата ddd.yyyyГК , определится суммой:
| yyyyГК = (400 • Q400 ГК + 100 • Q100 ГК + 4 • Q4 ГК + Q1 ГК) г. |
(9.17) |
Выражение для второго члена tГК (yyyyГК – 1) результирующей правой части (9.12) найдём из (5.1) при N = (yyyyГК – 1) и K = 365:
| tГК (yyyyГК – 1) = 365 • (yyyyГК – 1) + floor [(yyyyГК – 1) / 4] – floor [(yyyyГК – 100) / 4] + floor [(yyyyГК – 1) / 400] |
(9.18) |
На основании (9.13) – (9.17), (8.3) и (9.12) с учётом (9.18) запишем алгоритм вычисления составляющих упрощённой даты ГК по значению t основной шкалы:
| Табл. 8 |
Алгоритм преобразования значений t основной шкалы
в упрощённые даты ГК |
| 1. |
Q400 ГК = floor [(t – 2) / 146097] |
| 2. |
Q100 ГК = floor [(t – 146097 • Q400 ГК – 2) / 36524] |
| 3. |
Q4 ГК = floor [(t – 146097 • Q400 ГК – 36524 • Q100 ГК – 2) / 1461] |
| 4. |
Q1 ГК = ceil [(t – 146097 • Q400 ГК – 36524 • Q100 ГК – 1461 • Q4 ГК – 2) / 365] |
| 5. |
yyyyГК = (400 • Q400 ГК + 100 • Q100 ГК + 4 • Q4 ГК + Q1 ГК) г. |
| 6. |
vГК (yyyyГК) = 1 – ceil [yyyyГК / 4 – floor (yyyyГК / 4)] + ceil [yyyyГК / 100 – floor (yyyyГК / 100)] – ceil [yyyyГК / 400 – floor (yyyyГК / 400)] |
| 7. |
dddГК = t – 365 • (yyyyГК – 1) – floor [(yyyyГК – 1) / 4] + floor [(yyyyГК – 100) / 4] – floor [(yyyyГК – 1) / 400] – vГК (yyyyГК) – 2 |
|
| |
Таким образом, используя алгоритмы, содержащиеся в табл. 6, 7, 8, любой момент времени t основной шкалы можно перевести в упрощённые даты любого календаря, а затем по соотношениям из табл. 4, 5 (или по таблицам Приложения) – в обычные даты. Момент завершения найденной даты будет соответствовать значению t, указывающему порядковый номер суток, отсчитываемых от нулевой отметки t = 0 основной шкалы времени и завершающихся в этот момент.
10. Дни недели ↑
Создадим алгоритм, с помощью которого сопоставим значениям основной шкалы времени дни недели. Если предположить, что на протяжении обозримого исторического периода последовательность смены дней недели сохранялась такой же, каковой она является сегодня, то для решения этой задачи достаточно привязать недельный семисуточный цикл к любой дате сегодняшнего календаря и найти значение этой даты на шкале времени. Для привязки удобно выбрать дату, на которую приходится воскресенье, а дни недели последовательно пронумеровать, начиная с воскресенья, которому присвоим нулевой номер, табл. 9:
| Табл. 9 |
| Воскресенье (Вс) |
0 |
| Понедельник (Пн) |
1 |
| Вторник (Вт) |
2 |
| Среда (Ср) |
3 |
| Четверг (Чт) |
4 |
| Пятница (Пт) |
5 |
| Суббота (Сб) |
6 |
|
| |
В качестве привязки выберем, например, такую известную дату как 22 июня 1941 г. – начало Великой Отечественной войны, на которую приходилось воскресенье. По соотношению из табл. 4 для июня (шестой месяц) переведём эту дату в упрощённую:
| ddd = dd + 151 = 22 + 151 = 173 |
Учитывая, что 1941 г. – простой (vГК (1941) = 0) и воспользовавшись соотношением (8.13) для ГК, найдём значение привязки шкалы времени к воскресенью, соответствующее этой дате:
| tПрив.(173.1941) = 365 • (1941 – 1) + floor [(1941 – 1) / 4] – floor [(1941 – 1) / 100] + floor [(1941 – 1) / 400] + vГК (1941) + 173 + 2 = |
| = 365 • 1940 + floor (1940 / 4) – floor (1940 / 100) + floor (1940 / 400) + 173 + 2 = 708100 + 485 – 19 + 4 + 173 +2 = 708745 |
Увеличивая или уменьшая значение tПрив.= 708745 на любое число кратное 7 (недельному циклу) в результате будем получать значения номеров суток шкалы, на которые будут приходиться воскресенья. А разность между любым значением t шкалы и значением tВс предш. предшествующего воскресенья укажет номер дня недели для этого значения t в соответствии с табл. 9. Обозначив номер дня недели символом «day», составим соотношение:
| day = t – tВс предш.= t – 7 • floor [(t – 708745) / 7] – 708745 |
(10.1) |
Очевидно, что такую привязку можно с равным успехом осуществить по любому значению t основной шкалы, на которое приходится воскресенье. Для удобства целесообразно минимизировать tПрив. по абсолютной величине. Это легко сделать, уменьшив его на максимальное число кратное 7, но меньшее 708745. Таким числом является 708743 (делится на 7 без остатка: 708743 / 7 = 101249). После преобразования получим эквивалентное (10.1) упрощённое соотношение:
| day = t – 7 • floor [(t – 2) / 7] – 2 |
(10.2) |
Здесь tПрив. = 2 сут – момент завершения 2-х суток основной шкалы времени, на которые приходится воскресенье.
11. Диапазоны применимости календарей и отображение дат до Нашей эры ↑
Итак, были рассмотрены три календаря – ВК, ЮК, ГК, которые в различные эпохи действовали в Европе и в России. Обозначим временны́е диапазоны, в пределах которых исторические события могли быть датированы по каждому их этих календарей современниками этих событий.
Проще всего дело обстоит с ГК. Нижней границей диапазона фактического действия ГК следует считать дату, которой обозначено начало его применения – 15.10.1582 ГК (раздел 5). Сегодня ГК является календарём, действующим в большинстве стран мира, и отменять его пока никто не намеревается. Поэтому верхняя граница ГК отсутствует. Считаем, что ГК продолжается в неопределённое будущее без ограничения. Диапазон дат, начиная от 15.10.1582 ГК без ограничения сверху, будем считать периодом фактического действия ГК.
Перейдём к ЮК. Здесь ситуация менее определённая. С одной стороны, можно считать, что официально ЮК прекратил существование с даты ввода в действие ГК, т. е. после 04.10.1582 ЮК. Но, с другой стороны, даже европейские государства продолжали использовать ЮК ещё полтора столетия. После григорианской реформы католические государства в течение несколько лет отказались от ЮК и перешли на уточнённый ГК. Ещё в течение ближайших полутора веков и протестантские государства перестали использовать ЮК. Процесс перехода затянула Англия, принявшая ГК начиная с даты 14.09.1752 ГК, которая заменила дату 03.09.1752 ЮК. Переход через столетний рубеж 1700 г. увеличил смещение дат между ЮК и ГК на сутки и вместо 10 сут пришлось добавить 11 сут.
Но в России ЮК был лишь введён начиная с даты 01.01.1700 ЮК и официально действовал ещё более двух веков, несмотря на то, что большинство развитых стран от него уже отказались в силу его ошибочности. Малограмотность российской знати, следовавшей православным канонам, была столь глубока, что ввести ГК не решился даже Пётр I, ограничившись косметическим изменением. Попытки ввести ГК неоднократно предпринимались российскими учёными вплоть до 1910 г. ЮК, но все они наталкивались на сопротивление власти и РПЦ. Лишь после Октябрьской социалистической революции был принят декрет от 24.01.1918 ЮК о переходе на ГК. Декрет предписывал дату 01.02.1918 ЮК заменить датой 14.02.1918 ГК. Переход через три столетних рубежа 1700, 1800, 1900 гг. увеличил смещение дат между ЮК и ГК на трое суток и вместо 10 сут было добавлено 13 сут. Исходя из этого, верхним значением диапазона фактического действия ЮК будем считать дату 31.01.1918 ЮК, которая предшествовала дате его официальной отмены в России.
Сложнее определиться с датой начала действия ЮК. Эра от «РХ» была изобретена в 525 г. н. э. монахом Дионисием Малым в противовес действовавшему в Риме календарю по эре Диоклетиана. И хотя счёт лет от «РХ» внедрялся медленно (ЮК от «РХ» получил распространение лишь через три столетия после его изобретения), условно примем за начало фактического действия ЮК следующий после его изобретения 526 г. н. э., а диапазон дат от 01.01.0526 ЮК до 31.01.1918 ЮК будем считать периодом фактического действия ЮК.
Похожая ситуация с ВК. Датой завершения фактического действия ВК можно считать дату, предшествующую дате, обозначенной указом Петра I о замене ВК на ЮК (раздел 7), т. е. 31 дек. 7208 ВК. Но с датой начала фактического применения ВК неопределённость ещё большая, чем с ЮК. Существует лишь не очень надёжная т. з., что начало официальному применению ВК положил Никейский собор, проходивший в 325 г. ЮК, который соответствует 5833 г. ВК. Не остаётся ничего другого, как принять за начало действия ВК начало следующего года, т. е. дату 01 сен. 5834 ВК, а диапазон дат от 01 сен. 5834 ВК до 31 дек. 7208 ВК считать периодом фактического действия ВК.
Понятно, что принятые диапазоны фактического действия рассматриваемых календарей условны и при необходимости могут быть расширены как в будущее, так и в прошлое на любые периоды времени путём экстраполяции. И если экстраполяция в будущее вышедших из употребления календарей бессмысленна (вменяемые люди по этим календарям ничего датировать уже не будут), то экстраполяция в прошлое полезна для приведения к единообразию датировок, указанных разными историками разных эпох по разным календарям. Календари, экстраполированные в прошлое при сохранении их структуры и привязки, называются пролептическими. Любой из рассмотренных календарей может быть дополнен пролептической составляющей. Но исторически сложилось так, что наибольшее распространение получил пролептический ЮК.
Начало пролептическому ЮК положил ещё Дионисий Малый. Создав счёт годов от «РХ», он фактически экстраполировал ЮК в прошлое до условной даты «РХ». В XVIII в. н. э. эта экстраполяция в прошлое была продолжена на неограниченный период ранее этой даты. Имеются два варианта пролептической экстраполяции ЮК: астрономическая – ЮК (аст.) и историческая – ЮК (ист.), рис. 17.
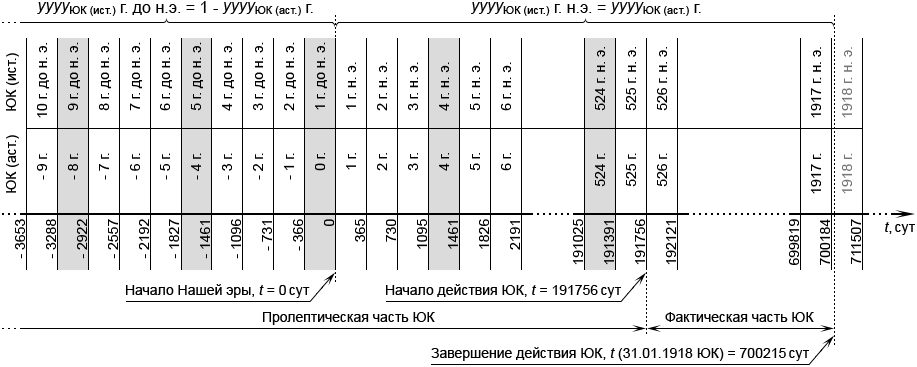 |
|
Рис. 17. Пролептические экстраполяции ЮК (аст.) и ЮК (ист.)
Первый ряд сверху – номера годов ЮК (ист.).
Второй ряд сверху – номера годов ЮК (аст.).
Внизу – шкала времени с отметками моментов завершения годов, сут.
Високосные годы отмечены затемнённым фоном.
|
Пролептическая часть ЮК (аст.) строится в соответствии с правилами арифметики: 526-му г., принятому за начало фактического действия ЮК, предшествует год, имеющий номер 525 г. Номера каждого более раннего года последовательно уменьшаются на единицу до года, имеющего номер 1 г., которому предшествует год, имеющий номер 0 г. Ещё более ранние годы последовательно нумеруются отрицательными числами: -1 г., -2 г., -3 г. и т. д.
Годы пролептической части ЮК (ист.) в прошлое от 526-го г. до 1-го г. нумеруются аналогично пролептической части ЮК (аст.). Поэтому в интервале от 1-го г. до 526-го г. и далее в будущее (без ограничения сверху) номера годов и даты обоих вариантов совпадают. Но нумерация годов ЮК (ист.), предшествующих 1-му г., отличается от нумерации принятой для ЮК (аст.). В ЮК (ист.) отсутствует нулевой год и не используются отрицательные числа. Году, имеющему 1-й номер, предшествует год, имеющий тоже 1-й номер, но обозначаемый как год «до Нашей эры» (сокращённо – «до н. э.») – 1 г. до н. э. Далее в прошлое: 1-му г. до н. э. предшествует 2 г. до н. э., 2-му г. до н. э. предшествует 3 г. до н. э., и т. д. без ограничения в прошлое. Даты и указания на эпохи по ЮК (ист.), относящиеся к периоду ранее 1 г., всегда дополняются обозначением «до н. э.». При указании дат по ЮК (ист.), начиная с 1 г. в будущее, номера годов следует дополнять обозначением «н. э.», указывающим на принадлежность даты к Нашей эре. Но на практике обозначение «н. э.» порой опускается, что может привести к путанице. Не всегда понятно, по какому календарю – ЮК или ГК – указана дата, поскольку разница между датами составляет не более 13 сут, вследствие чего датировки неотличимы по эпохе, а их записи идентичны. Это обстоятельство следует иметь в виду особенно для периода, когда действовали оба календаря.
Для любого года, предшествующего 1-му г. н. э., номер года по ЮК (ист.) всегда на единицу больше абсолютной величины номера этого же года по ЮК (аст.). Это можно отобразить соотношениями
| yyyyЮК (ист.) г. до н. э. = 1 – yyyyЮК (аст.) г. |
(11.1) |
| yyyyЮК (аст.) г. = 1 – yyyyЮК (ист.) г. до н. э. |
(11.2), |
действующими при yyyyЮК (аст.) г. ≤ 0 и при любых yyyyЮК (ист.) г. до н. э.
Порядок следования месяцев и номеров суток внутри месяцев для годов пролептической части обоих вариантов ЮК не изменяется. Любой год, имеющий номер yyyy, вне зависимости от знака номера по ЮК (аст.) или от наличия обозначения «до н. э.» по ЮК (ист.), начинается с даты 01.01.yyyy (01 янв. yyyy) и, в обычном порядке последовательно пробегая все месяцы и номера суток внутри месяцев, завершается датой 31.12.yyyy (31 дек. yyyy).
Для дат до н. э. по ЮК (ист.) имеет место неоднозначность при определении типа года – простой или високосный. Правило юлианского приближения требует, чтобы промежуток между двумя ближайшими високосными годами состоял из трёх простых годов. На практике это правило трансформировалось в условие кратности номеров годов числу 4: если номер года делится на 4 без остатка, год – високосный. Это условие можно записать следующим образом:
| yyyyЮК / 4 = floor (yyyyЮК / 4) |
(11.3) |
Это соотношение применимо для любых дат по ЮК (аст.), но по ЮК (ист.) – лишь для дат н. э., т. е. в будущее, начиная от даты 01.01.0001 н. э. Отсутствие нулевого года в ЮК (ист.) приводит к тому, что для дат до н. э., т. е. из прошлого, завершая датой 31.12.0001 до н. э., это условие не работает, а високосными следует считать годы, имеющие номер на единицу больший, чем определяемый из (11.3). Для дат до н. э. по ЮК (ист.) условие високосности года приобретает вид:
| (yyyyЮК (ист.) г. до н. э. – 1) / 4 = floor [(yyyyЮК (ист.) г. до н. э. – 1) / 4] |
(11.4) |
Високосные годы до н. э. по ЮК (ист.) будут иметь номера: 1, 5, 9 и т. д. (см. рис. 17).
Соотношения разделов 8 – 10 в полной мере применимы к операциям с датами при отрицательных значениях годов ЮК (аст.) так же, как и с обычными датами ГК, ВК и упрощёнными датами ЮК, ГК, ВК, если они строятся по правилам арифметики. Но для операций с датами до н. э. по ЮК (ист.) эти соотношения неприменимы. Для операций с датами до н. э. по ЮК (ист.) имеет смысл, используя (11.1) и (11.2), преобразовать номер года ЮК (ист.) в номер года ЮК (аст.), произвести необходимые действия и вернуться к дате ЮК (ист.). Вообще, ЮК (аст.) строже, однозначнее и потому предпочтительней, чем ЮК (ист.). Но историки предпочитают традиционно использовать ЮК (ист.). В настоящей статье эта традиция сохранена лишь в нескольких случаях, не требующих строгости.
12. Программа пересчёта дат ↑
Программа написана на языке «JavaScript» и работает в браузере на машине клиента, не используя ресурсы сервера. С сервера производится только её загрузка. По ссылке prog.htm программа загружается в оперативную память и открывается страница запуска программы (в новом окне или в новой вкладке в зависимости от браузера и его установок), содержащая кнопку «Запуск программы» и настоящее описание работы с программой. При работе с программой эту страницу (вкладку) не следует закрывать. Её закрытие приведёт к выгрузке программы из оперативной памяти и все полученные результаты расчётов будут утеряны. Работа программы проверялась в браузерах Internet Explorer 8.0.6001.18702, Google Chrome 44.0.2403.107 m, Opera 30.0.1835.125, Firefox 39.0.
При нажатии на кнопку «Запуск программы» откроется рабочее окно (или вкладка), в котором отобразится таблица ввода исходных дат, рис. 18. Над таблицей – ряд выключателей, указывающих календари, по которым возможно будет вводить исходные даты для расчёта, а рассчитанная информация будет выводиться на экран в таблицу «Результаты». Отключив любые из них и нажав кнопку «Повторить вывод», можно избавиться от визуализации лишних колонок обеих таблиц, мешающих восприятию. Всегда остаётся включённой левая колонка, отображающая шкалу времени («Шкала вр.»). Вне зависимости от положения выключателей, расчёт производится по всем календарям и вся рассчитанная информация хранится в оперативной памяти. Включив ранее отключённые колонки и ещё раз повторив вывод, можно вновь отобразить ранее рассчитанные результаты по всем календарям.
При запуске программы и после каждого акта расчёта фокус ввода устанавливается в колонке «Шкала вр.» и может быть перемещён вправо клавишей «Tab» и обратно сочетанием клавиш «Shift»+«Tab» или установлен в нужное поле ввода курсором мыши.
В соответствующие колонки даты можно вводить как в обычном формате с указанием месяца и номера суток внутри месяца, так и в упрощённом формате (раздел 8) – без указания месяца, используя лишь номер года и номер суток внутри года. В программе используется компьютерный вариант отображения дат. Слева направо: для обычных дат – номер года (yyyy), номер (для ВК – название) месяца (mm, мес.), номер суток месяца (dd); для упрощённых дат – номер года (yyyy), номер суток года (ddd). Такой порядок принят для того, чтобы исключить ввод некорректного номера суток. Для обычных дат после ввода номера года (yyyy) и месяца (mm, мес.) программа не позволит ввести 31-й номер суток месяца, состоящего из 30 суток, или 29 февраля в простом году. Для упрощённых дат после ввода номера года (yyyy) – не позволит ввести нулевой номер суток в простом году. При попытке этот порядок изменить, программа выведет предупреждение и потребует его соблюдения.
В поля «t, сут», «yyyy», «ddd», «mm», «dd» могут быть введены только числовые значения. Максимальное количество вводимых знаков, первый из которых может быть «минус», для значений шкалы времени составляет восемь, а для номеров года (yyyy) всех календарей, кроме ЮК (ист.), – пять. Для ЮК (ист.) количество знаков номера года ограничено значением четыре, поскольку роль знака «минус» для него выполняет обозначение «до н. э.». Для УпрВК и ВК номера годов ограничены только положительными значениями. Номера месяцев, отображаемых числами (mm), ограничены значениями от 1 до 12 включительно. Номера суток (ddd) упрощённых дат в зависимости от типа введённого года (простой или високосный) ограничены значениями от 0 или от 1 до 365 включительно. Номера суток (dd) обычных дат – значениями от 1 до 28, 29, 30, 31 в зависимости от введённых месяца и года. При попытке ввести значения, выходящие за указанные пределы, программа выведет сообщение об ошибке и фокус будет возвращён в поле, в котором эта ошибка была совершена. Обозначения «н. э.» или «до н. э.» для дат по ЮК (ист.) и название месяца («мес.») для дат по ВК выбираются курсором из выпадающих списков. После полного завершения ввода даты по ЮК (ист.) изменение обозначений «н. э.» или «до н. э.» становится недоступным. Чтобы это изменение вновь стало доступным, необходимо нажать кнопку «Отменить ввод». Нажатие этой кнопки удаляет все введённые значения из всех полей и возвращает таблицу ввода дат в исходное состояние.
Имеются ещё два ограничения по значениям шкалы времени: минимальное – отрицательное значение -2011918, соответствующее первым суткам первого года по ВК, и максимальное – положительное значение 3652061, соответствующее последним суткам 9999 г. по ГК. При попытке выхода за эти пределы по шкале времени или по датам, приводящим к такому выходу, программа выведет предупреждение и таблица ввода вернётся в исходное состояние. На самом деле, попытки сопоставления дат по представленным календарям даже ранее 326 г. н. э. бессмысленны, поскольку ни одного из этих календарей до этого года не существовало. До 326 г. н. э. имеют смысл лишь даты по ЮК, которые присваивались историческим событиям постфактум после создания его пролептической части (раздел 11). Переводить будущие даты действующего ГК в даты календарей вышедших из употребления вообще не имеет смысла. Но для желающих позабавиться сохранена возможность поиграть датами на семь тысяч лет назад и на восемь тысяч лет вперёд от наших дней. С учётом всех ограничений, наиболее ранние и наиболее поздние значения вводимых дат, которые программа примет к исполнению, по всем календарям приведены в верхней и нижней строках табл. 10.
При работе в IE ввод значения в каждое поле следует завершать нажатием клавиши «Tab», в Chrome, Opera, Firefox – клавиши «Enter». Незначащие (предваряющие) нули вводить не требуется, при завершении ввода каждого значения программа сформирует их автоматически. После завершения ввода корректного значения шкалы времени или полной исходной даты, фокус устанавливается на кнопку «Рассчитать», и расчёт может быть запущен клавишей «Enter» или нажатием на эту кнопку курсором. После расчёта хотя бы одного значения, ниже таблицы ввода появляется таблица «Результаты», содержащая строку с результатами расчёта по всем календарям, включённым для отображения, а программа становится готова к вводу нового значения для расчёта. Результат каждого последующего расчёта располагается выше предшествующего и отделяется от него пустой строкой, смещая все предшествующие результаты на две строки вниз. После появления хотя бы одного рассчитанного результата становится доступной опция «Рассчитать диапазон». Включение этой опции позволяет рассчитать диапазон дат, начиная от последней (самой верхней) ранее рассчитанной даты до даты, введённой непосредственно перед включением этой опции. При этом вводимая дата должна быть более поздней, чем рассчитанная ранее. Результаты расчёта диапазона отображаются единым массивом без пустых строк. Направление оси времени внутри такого массива – снизу вверх: нижняя строка – дата начала диапазона (рассчитанная ранее), верхняя строка – дата завершения диапазона (введённая непосредственно перед включением опции). Последняя (самая поздняя) дата диапазона может быть использована для продолжения расчёта диапазона в будущее.
Результаты расчётов выводятся шрифтами, форматы которых отображены в табл. 10. Значения шкалы времени на всём протяжении – обычным прямым. Обычные даты, входящие в диапазон фактического действия соответствующего календаря (раздел 11), – полужирным прямым. Обычные даты, не входящие в диапазон фактического действия соответствующего календаря, – осветлённым прямым кроме пролептических частей ЮК (аст.) и ЮК (ист.). Обычные даты пролептических частей ЮК (аст.) и ЮК (ист.) – обычным прямым. Упрощённые даты в пределах диапазона фактического действия соответствующего календаря и в пролептической части ЮК – обычным курсивом, вне этих пределов – осветлённым курсивом. Дни недели – обычным прямым.
При отрицательных значениях t шкалы времени упрощённые даты ЮК (УпрЮК) строятся на основе астрономического варианта ЮК, т. е. годы дат УпрЮК имеют отрицательные номера, совпадающие с номерами годов ЮК (аст.), а обозначения «н. э.» и «до н. э.» не применяются. Упрощённые даты ГК (УпрГК) построены аналогично.
| Табл. 10 |
| |
Шкала
времени |
УпрГК
yyyy . ddd |
ГК
yyyy . mm . dd |
УпрЮК
yyyy . ddd |
ЮК (аст.)
yyyy . mm . dd |
ЮК (ист.)
(эра) yyyy . mm . dd |
УпрВК
yyyy . ddd |
ВК
yyyy month dd |
День
нед. |
|
| |
3652061 |
9999 . 365 |
9999 . 12 . 31 |
9999 . 292 |
9999 . 10 . 19 |
(н.э.) 9999 . 10 . 19 |
15508 . 048 |
15508 окт. 19 |
Пт. |
|
| |
↑
Обычный
прямой
↓ |
↑
Обычный
курсив
↓ |
↑
Полужирный
прямой
↓ |
↑
Осветлённый
курсив
↓ |
↑
Осветлённый
прямой
↓ |
↑
Осветлённый
прямой
↓ |
↑
Осветлённый
курсив
↓ |
↑
Осветлённый
прямой
↓ |
↑
Обычный
прямой
↓ |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
1918 . 032 |
1918 . 02 . 01 |
(н.э.) 1918 . 02 . 01 |
|
| |
1918 . 031 |
1918 . 01 . 31 |
(н.э.) 1918 . 01 . 31 |
|
| |
↑
Обычный
курсив
↓ |
↑
Полужирный
прямой
↓ |
↑
Полужирный
прямой
↓ |
|
| |
7208 . 122 |
7208 янв. 01 |
|
| |
7208 . 121 |
7208 дек. 31 |
|
| |
1582 . 288 |
1582 . 10 . 15 |
↑
Обычный
курсив
↓ |
↑
Полужирный
прямой
↓ |
|
| |
1582 . 287 |
1582 . 10 . 14 |
|
| |
↑
Осветлённый
курсив
↓ |
↑
Осветлённый
прямой
↓ |
|
| |
|
| |
0526 . 01 . 01 |
(н.э.) 0526 . 01 . 01 |
|
| |
0525 . 12 . 31 |
(н.э.) 0525 . 12 . 31 |
|
| |
↑
Обычный
прямой
↓ |
↑
Обычный
прямой
↓ |
|
| |
5834 . 001 |
5834 сен. 01 |
|
| |
5833 . 365 |
5833 авг. 31 |
|
| |
↑
Осветлённый
курсив
↓ |
↑
Осветлённый
прямой
↓ |
|
| |
|
| |
|
| |
|
| |
-2011918 |
-5508 . 200 |
-5508 . 07 . 19 |
-5508 . 244 |
-5508 . 09 . 01 |
(до н.э.) 5509 . 09 . 01 |
0001 . 001 |
0001 сен. 01 |
Сб. |
|
|
| |
Для удаления всех результатов расчётов из рабочего окна его необходимо закрыть, вернуться на страницу (вкладку) запуска программы, перезагрузить её («refresh», «F5») и перезапустить программу кнопкой «Запуск программы».
Поскольку программа работает на машине пользователя, время расчёта и время вывода результатов на экран могут существенно различаться в зависимости от браузера и мощности машины. В любом случае, время вывода результатов в сотни раз больше, чем время расчёта. При проверочном расчёте диапазона значений из 5 тыс. сут (~14 годов) на машине небольшой мощности время расчёта во всех браузерах составило доли секунды, время вывода на экран в IE ~75 сек, в Chrome и Opera ~ 20 сек, в Firefox 4,5 сек. В диапазоне из 20 тыс. сут (~55 годов) в IE расчёт занял ~1,8 сек, вывод на экран ~5 мин, в Chrome и Opera расчёт занял ~0,4 сек, вывод на экран ~6 мин. При попытках в этих трёх браузерах увеличить диапазон расчёта далее, за разумное время дождаться завершения операций не удалось. Значительно лучшие результаты показал Firefox: расчёт диапазона из 80 тыс. сут (~220 годов) занял ~0,25 сек, вывод на экран ~2 мин. При желании пользователя оценить эти параметры на своей машине, можно задействовать опцию «Отобразить время расчёта и вывода». Следует иметь в виду, что после каждого акта расчёта (даже единичного значения) или после нажатия кнопки «Повторить вывод» рабочее окно полностью перезагружается. Поэтому время вывода результатов на экран после расчёта или перезагрузки – это время вывода всей хранящейся в оперативной памяти информации, включая результаты, рассчитанные ранее. В зависимости от браузера и настроек, при расчётах больших диапазонов могут появляться системные оповещения с предложением прервать или продолжить работу сценария. При продолжении, время ожидания реакции пользователя с неизбежностью добавляется к значению времени вывода результатов на экран.
Рабочее окно программы – окно виртуальное. Оно строится в оперативной памяти методами «JavaScript» и не связано с конкретным файлом. При использовании таких окон, в браузерах предусмотрены разные ограничения для обеспечения безопасности пользователя. В частности, ограничивается возможность создания файлов для сохранения содержания таких окон на жёстком диске. В связи с этим, имеются неудобства при необходимости сохранить результаты расчётов. Из перечисленных браузеров сохранить содержимое рабочего окна с результатами расчётов в файл обычным путём (через меню «Файл») позволил только Firefox. При работе в IE эту возможность обеспечивает специальная кнопка «Сохранить (IE)», расположенная под таблицей ввода данных. Но в Chrome и Opera оба эти варианта не работают. В этих браузерах результаты расчёта проще всего сохранить выделив («Ctrl»+«A») и скопировав («Ctrl»+«C») всё содержимое рабочего окна в буфер обмена, а затем вставить это содержимое в пустую страницу MS Word, удалив затем таблицу ввода данных, которая на странице MS Word отображается некорректно. Таблица полученных результатов отображается в MS Word вполне корректно и может быть сохранена в файл обычным путём.
Поскольку автор – не программист, то вряд ли эта программа представляет собой «шедевр программного искусства» и может изменяться, совершенствоваться и распространяться любым желающим под его ответственность. Полный текст программы представлен в файле prog1.txt. Запуск на выполнение загруженной в оперативную память программы осуществляется вызовом функции «Page()», которая создаёт рабочее окно, что и происходит при нажатии кнопки «Запуск программы». Дальнейшее управление работой программы производится из рабочего окна.
13. Возможность календарной реформы будущего ↑
Итак, на сегодняшний день ГК используется в большинстве развитых государств и принят в мире для международного общения. В некоторых странах для внутреннего применения и по сей день используются другие календарные системы. Главное достоинство ГК в его структуре, которая построена таким образом, что отклонения моментов завершения любых КГ от моментов завершения соответствующих ТГ не превышают одних суток. Это позволяет ежегодно отображать сезонные реперные моменты одинаковыми (максимум, соседними) внутригодовыми датами. Но поскольку ГК формировался на протяжении тысячелетий, он содержит неудобства, сложившиеся в древности, которые по сегодняшним представлениям являются бессмысленными анахронизмами. Главное неудобство – разбиение КГ на 12 месяцев, продолжительность которых бессистемно меняется от 28 до 31 сут. Второе – семидневный недельный цикл не кратный ни количеству суток в КГ, ни количеству суток в месяцах. Месяц от месяца и год от года дни недели «скользят» по датам. В связи с этим предлагались и продолжают предлагаться различные проекты реформы календаря, устраняющие эти неудобства. В качестве примера – один из удачных проектов.
Основная часть КГ продолжительностью 364 сут делится на 4 квартала по 91 сут. Каждый квартал делится на 3 месяца, первый из которых содержит 31 сут, два последующих – по 30 сут. Продолжительность квартала становится кратна 7, что позволяет начинать все кварталы всех КГ с понедельника, а завершать воскресеньем. Первые сутки каждого КГ не включаются в счёт кварталов, месяцев и недель и объявляются всеобщим нерабочим днём – праздником Нового года. В високосном КГ дополнительные сутки тоже объявляются всеобщим нерабочим днём, не включаются в счёт кварталов, месяцев и недель и вставляются после 30 июня.
Существуют и другие подобные проекты. Но все они наталкиваются на проблему ввода нового календаря в действие. В отличие от прошлых веков, сегодняшний мир информационно един. Поэтому для ввода нового календаря в действие требуется согласовать этот вопрос с подавляющим большинством государств и принять по этому поводу обязательное к исполнению международное решение. Но даже после принятия такого решения, ещё в течение как минимум поколения, в головах людей будет путаница на бытовом уровне. Поскольку по структуре и по написанию старые и новые даты будут идентичны, то до тех пор, пока не уйдёт поколение, прожившее часть жизни при старом календаре, придётся указывать по какому – старому или новому – календарю произведена каждая конкретная датировка. Вряд ли мировое сообщество в ближайшем будущем возьмётся за решение этого вопроса.
Но имеется возможность избежать сложности ввода календаря в действие. Для этого надо предложить такой проект, который исключил бы путаницу между старыми и новыми обозначениями дат по структуре и написанию. Это легко сделать, если отказаться от использования в календаре месяца. По сути месяц – лишняя переменная, не несущая полезной информации и включённая в календарь искусственно, – попытка связать между собой три периода: период обращения Земли вокруг Солнца, период обращения Земли вокруг оси и период обращения Луны вокруг Земли. Но календарь создавался для того, чтобы отображать одинаковыми внутригодовыми датами реперные моменты, определяющие сезонные изменения, происходящие на Земле в течение ТГ. Движение Луны к сезонным изменениям отношения не имеет. Эти изменения зависят только от положения Земли на солнечной орбите, которое определяется временем, прошедшим от условного момента, принятого за нулевой, до текущего момента. Поэтому в календаре достаточно использовать продолжительности лишь двух периодов: КГ, в среднем приближенного к ТГ, и средних солнечных суток, приближенных к средней продолжительности истинных солнечных суток. Применение месяца, как промежуточной единицы времени, излишне. Такая промежуточная единица имела смысл в эпохи, когда основная масса населения не умела оперировать числами более, чем в несколько десятков. Но сегодняшнее население достаточно хорошо умеет считать (скажем, деньги) не только сотнями, но тысячами и миллионами. И досчитать до 365, до максимального номера суток года, ни для кого не составит труда.
И если создать календарь на основе сквозной нумерации суток внутри года, как описано в разделе 8, то указанная проблема ввода такого календаря в действие будет решена. Любая дата будет состоять лишь из двух чисел: номера года и номера суток внутри года. Счёт номеров годов следует продолжить в соответствии с текущими номерами сегодняшнего ГК. В течение ближайших почти восьми тысяч лет они будут обозначаться только четырёхзначными числами. А сутки внутри года будут обозначаться номерами от 0 или от 1 (в зависимости от типа года) до 365, т. е. не более, чем трёхзначными числами. Номера суток, содержащие менее трёх знаков, можно (хотя и не обязательно) дополнять до трёх знаков незначащими (предваряющими) нулями, подобно тому, как в сегодняшнем ГК номера суток внутри месяца и номера месяцев часто дополняют незначащим нулём до двух знаков. Таким образом, возможность путаницы исчезнет – сразу будет понятно, что дата из двух составляющих, разделённых между собой точкой, косой чертой или дефисом, – это дата «нового» календаря, явно отличающаяся от дат «старого» календаря из трёх составляющих, включающая номер (или название) месяца. При записи «новых» дат порядок следования номеров годов и номеров суток внутри года может быть любым. Здесь путаницы тоже не будет. Вне зависимости от порядка следования, номера годов всегда будут отображаться четырёхзначными числами, а номера суток – не более, чем трёхзначными.
Предлагаемый вариант не является новшеством. Сквозная нумерация суток внутри года издавна применялась в астрономии и навигации. Например, приближённое значение разности между истинным и средним солнечным временем («уравнение времени») может быть вычислено по соотношению, включающему номер суток от начала года. Хотя, вне зависимости от типа года в астрономии нумерацию суток, как правило, начинают с единицы. При этом последние сутки високосного года получают номер 366. Но для календаря использование нулевого номера суток в високосном году удобнее. Как было показано (раздел 8), в этом случае сопоставление упрощённых дат с обычными не будет зависеть от типа года на протяжении 10 месяцев – от 01 марта по 31 декабря. Вне зависимости от типа года, дате 01 марта всегда будут соответствовать сутки номер 060, а 31 декабря – номер 365. Если же нумерацию суток високосного года тоже начать с единицы, то номером 060 будет обозначено 29 февраля, а 01 марта получит номер 061, увеличивая на единицу все последующие номера суток до конца года.
Если проект такой календарной реформы когда-нибудь будет рассматриваться всерьёз, то, как и в описанном в начале раздела примере, сутки любого года, имеющие номер 001, следует объявить всеобщим нерабочим днём – праздником Нового года, который не будет обозначаться никаким днём недели. Первым рабочим днём года становится понедельник, приходящийся на сутки номер 002, вторым – вторник, приходящийся на сутки номер 003. И т. д., до конца года. Поскольку недельный цикл будет распространён только на оставшиеся 364 сут (число кратное семи), то на последние сутки года, имеющие номер 365 (31 декабря), всегда будет приходится воскресенье. В високосном году сутки, предшествующие Новому году и имеющие номер 000, следует объявить ещё одним нерабочим днём – праздником Високосного года, который тоже не будет обозначается никаким днём недели. Так же, как и в простом году, первым рабочим днём становится понедельник, приходящийся на сутки номер 002. Далее до конца года структура дат и дней недели високосного года будет полностью повторять структуру дат и дней недели простого года, завершаясь последними сутками под номером 365, на которые будет приходиться воскресенье. Любой КГ может быть разделён на кварталы, состоящие из 91 сут., разбивка которых по «новым» и «старым» внутригодовым датам приведена в табл. 11. Каждый квартал будет начинаться в понедельник и завершаться воскресеньем.
| Табл. 11 |
| № кв. |
Упрощённые даты |
Обычные даты |
| I |
002 – 092 |
02(03) янв. – 02 апр. |
| II |
093 – 183 |
03 апр. – 02 июля |
| III |
184 – 274 |
03 июля – 01 окт. |
| IV |
275 – 365 |
02 окт. – 31 дек. |
|
| |
Понятно, что в полном объёме ввести такой календарь в действие возможно лишь официальным путём, поскольку изменения структуры недельного цикла и праздников влияют на трудовой режим общества. Но если не затрагивать недельный цикл и праздники, то использование главного преимущества предлагаемого календаря – отсутствие путаницы между «новыми» и «старыми» датами – предоставляет возможность частичного ввода его в обиходное употребление «явочным порядком», минуя не только международные соглашения, но и вообще какие-либо согласования с властью. Никто не может помешать людям при общении между собой указывать прошедшие, текущие или будущие даты порядковыми номерами суток внутри года. Вначале это может походить на забаву, которая при сегодняшней всеобщей компьютерной оснащённости легко осуществима. В качестве иллюстрации в правом верхнем углу этой страницы имеется календарь, построенный на основе такой последовательной нумерации суток внутри года. В верхней строке – текущее время hh:mm:ss и текущая дата в «новом» отображении ddd.yyyy. Во второй строке – день недели и дата в привычном отображении dd.mm.yyyy по сегодняшнему действующему календарю. Эта простенькая программка на «JavaScript» работает без обращения к внешним серверам времени. Дата и время отображаются в соответствии с текущими датой и временем машины пользователя. Текст программки приведён в файле prog2.txt и может быть использован в качестве такой забавы всеми желающими без ограничений.
Со временем такая забава может закрепиться и перерасти в традицию. И нельзя исключить, что кто-либо из «власть имущих» примет разумное решение и «повелит» такую традицию узаконить. Вдруг кто-то из них пожелает уподобиться Юлию Цезарю или папе Григорию XIII и прославить своё имя в веках?
1 Строго говоря, за центр координат следовало бы принять центр масс всей Солнечной системы, поскольку и Земля, и все планеты, и Солнце вращаются именно вокруг этого общего центра масс. Кроме того, если рассматривать процесс вращения Земли вокруг Солнца в системе координат, связанной с «неподвижными» удалёнными звёздами, то, вследствие прецессии земной оси, в такой «звёздной» координатной системе ЛЭЭ медленно вращается в плоскости эклиптики, совершая полный оборот примерно за 26 тысяч лет. Таким образом, выбранная система координат (x, y) в строгом смысле не является инерциальной и сама вращается и относительно центра масс Солнечной системы, и относительно звёзд.
Но масса Солнца составляет 99,9 % массы всей Солнечной системы. Поэтому центр масс Солнечной системы практически совпадает с центром Солнца. А календарь создаётся для практических нужд людей, связанных с сезонными изменениями, которые зависят только от изменения положения Земли относительно Солнца, но не от положения Земли или её движения (вращения) относительно центра масс Солнечной системы или относительно звёзд. Поэтому для построения календаря выбор системы координат (x, y), центр которой совпадает с центром Солнца, а ось x всегда параллельна ЛЭЭ и вращается относительно звёзд, вполне оправдан.
2 Скорость изменения угла φ немного колеблется около некоторого среднего значения. Это обусловлено эллиптичностью орбиты Земли – отклонением её от строгой окружности. Но поскольку эти колебания одинаково повторяются при каждом обороте Земли вокруг Солнца, то на продолжительность тропического года, о которой здесь идёт речь, они не оказывают влияния. В то же время, этот фактор приходится учитывать при определении продолжительности суток, о чём пойдёт речь ниже.
3 Отсюда и название этой линии: по разные стороны ЛПД – разные даты. ЛПД – линия условная. В качестве ЛПД можно выбрать любой меридиан. Главной причиной, по которой в качестве ЛПД был выбран именно 180-й меридиан явилось то обстоятельство, что он нигде, кроме Антарктиды, не проходит по суше. Таким образом, не может сложиться ситуация, что в одном и том же населённом регионе по разные стороны от ЛПД были бы различные календарные даты. Вторая причина в том, что противоположный 180-му нулевой меридиан, от которого производится отсчёт долгот, проходит через авторитетнейшую в научном мире Гринвичскую обсерваторию. После многолетней дискуссии, окончательное решение по выбору 180-го меридиана в качестве ЛПД и по всей совокупности смежных вопросов было принято на Международной меридианной конференции в Вашингтоне в 1884 г.
В силу условности ЛПД, островные государства, через которые или вблизи которых проходит ЛПД, из соображений собственного удобства устанавливают на своей территории местные правила исчисления текущей даты. Таким образом, в некоторых регионах гражданская ЛПД проходит лишь вблизи 180-го меридиана, но не строго по нему.
4 Ещё в первой половине XX века 1/86400 часть средних солнечных суток была принята за эталон секунды. Таким образом, по тогдашнему определению эталона секунды продолжительность средних солнечных суток всегда в точности равнялась 86400 секундам. Но в средине XX века появился более стабильный прибор измерения времени – атомные часы. И с 1967 г. в качестве эталона секунды принят период, за который совершается 9192631770 переходов между двумя сверхтонкими уровнями основного состояния атома Cs-133. Именно такое значение было принято для того, чтобы согласовать новый эталон секунды с ранее использовавшимся эталоном, определённым по астрономическим наблюдениям. Но продолжительность средних солнечных суток постоянно возрастает в связи с замедлением вращения Земли вокруг оси из-за потерь энергии на приливы-отливы. Поэтому средние солнечные сутки, измеренные по новому более стабильному эталону, перестали точно равняться 86400 секундам. И для того, чтобы в гражданском обиходе сохранить продолжительность суток без применения дробных долей секунды, но при этом использовать шкалу времени, определяемую цезиевым эталоном, приходится один раз в несколько лет добавлять в какие-либо сутки секунду координации. В XXI веке секунда координации была добавлена 31.12.2005, 31.12.2008, 30.06.2012. В эти даты сутки имели продолжительность не 86400 сек, а на одну секунду больше – 86401 сек.
Таким образом, продолжительность суток тоже величина непостоянная. Но временно́е смещение, обусловленное этим непостоянством, столь незначительно (одна секунда в несколько лет), что необходимость корректировки календаря из-за него может проявиться лишь через сотни тысяч лет. Поэтому для построения календарных датировок будем считать продолжительность суток равной 86400 секундам.
5 Если явно не указано иное, исторические события, связанные с реформами юридического характера, произошедшие до появления григорианского календаря (раздел 5), датируются по историческому юлианскому календарю (раздел 11). Более поздние – по григорианскому.
6 В классической дискретной математике имеются операторы аналогичные оператору «floor», но они более громоздки в написании и менее удобны для популярной статьи.
7 Чтобы не загромождать текст второстепенными деталями, здесь и далее при рассмотрении возможных структурных схем календарей значения всех N полагаем положительными, N > 0. Поэтому имеем право вынести N из-под знака абсолютной величины.
8 Не имеет значения, что христианские организации празднуют Рождество не 01 января, а на неделю раньше – 25 декабря. Смещение нулевых отметок обеих шкал времени на 7 сут не меняет смещения в 2 сут этих отметок относительно друг друга. А поскольку исторически за начало года было принято 01 января, то для нашего анализа удобнее рассматривать смещение именно нулевых отметок шкал времени, т. е. начальных моментов самых первых суток года, принятого за первый год летосчисления, а не мифическую дату «РХ».
9 Системы датировок до начала Нашей эры имеют свои особенности, которые будут рассмотрены в разделе 11.
Приложение ↑
Соответствие обычных и упрощённых дат для ЮК и ГК
Для простых годов в период (включительно):
dd.mm.yyyy от 01.01.yyyy по 28.02.yyyy
ddd.yyyy от 001.yyyy по 059.yyyy |
01 (янв.)
| dd |
ddd |
| 01 |
001 |
| 02 |
002 |
| 03 |
003 |
| 04 |
004 |
| 05 |
005 |
| 06 |
006 |
| 07 |
007 |
| 08 |
008 |
| 09 |
009 |
| 10 |
010 |
|
| dd |
ddd |
| 11 |
011 |
| 12 |
012 |
| 13 |
013 |
| 14 |
014 |
| 15 |
015 |
| 16 |
016 |
| 17 |
017 |
| 18 |
018 |
| 19 |
019 |
| 20 |
020 |
|
| dd |
ddd |
| 21 |
021 |
| 22 |
022 |
| 23 |
023 |
| 24 |
024 |
| 25 |
025 |
| 26 |
026 |
| 27 |
027 |
| 28 |
028 |
| 29 |
029 |
| 30 |
030 |
| 31 |
031 |
|
|
02 (фев.)
| dd |
ddd |
| 01 |
032 |
| 02 |
033 |
| 03 |
034 |
| 04 |
035 |
| 05 |
036 |
| 06 |
037 |
| 07 |
038 |
| 08 |
039 |
| 09 |
040 |
| 10 |
041 |
|
| dd |
ddd |
| 11 |
042 |
| 12 |
043 |
| 13 |
044 |
| 14 |
045 |
| 15 |
046 |
| 16 |
047 |
| 17 |
048 |
| 18 |
049 |
| 19 |
050 |
| 20 |
051 |
|
| dd |
ddd |
| 21 |
052 |
| 22 |
053 |
| 23 |
054 |
| 24 |
055 |
| 25 |
056 |
| 26 |
057 |
| 27 |
058 |
| 28 |
059 |
|
|
|
Для високосных годов в период (включительно):
dd.mm.yyyy от 01.01.yyyy по 29.02.yyyy
ddd.yyyy от 000.yyyy по 059.yyyy |
01 (янв.)
| dd |
ddd |
| 01 |
000 |
| 02 |
001 |
| 03 |
002 |
| 04 |
003 |
| 05 |
004 |
| 06 |
005 |
| 07 |
006 |
| 08 |
007 |
| 09 |
008 |
| 10 |
009 |
|
| dd |
ddd |
| 11 |
010 |
| 12 |
011 |
| 13 |
012 |
| 14 |
013 |
| 15 |
014 |
| 16 |
015 |
| 17 |
016 |
| 18 |
017 |
| 19 |
018 |
| 20 |
019 |
|
| dd |
ddd |
| 21 |
020 |
| 22 |
021 |
| 23 |
022 |
| 24 |
023 |
| 25 |
024 |
| 26 |
025 |
| 27 |
026 |
| 28 |
027 |
| 29 |
028 |
| 30 |
029 |
| 31 |
030 |
|
|
02 (фев.)
| dd |
ddd |
| 01 |
031 |
| 02 |
032 |
| 03 |
033 |
| 04 |
034 |
| 05 |
035 |
| 06 |
036 |
| 07 |
037 |
| 08 |
038 |
| 09 |
039 |
| 10 |
040 |
|
| dd |
ddd |
| 11 |
041 |
| 12 |
042 |
| 13 |
043 |
| 14 |
044 |
| 15 |
045 |
| 16 |
046 |
| 17 |
047 |
| 18 |
048 |
| 19 |
049 |
| 20 |
050 |
|
| dd |
ddd |
| 21 |
051 |
| 22 |
052 |
| 23 |
053 |
| 24 |
054 |
| 25 |
055 |
| 26 |
056 |
| 27 |
057 |
| 28 |
058 |
| 29 |
059 |
|
|
|
Для любых годов в период (включительно):
dd.mm.yyyy от 01.03.yyyy по 31.12.yyyy
ddd.yyyy от 060.yyyy по 365.yyyy |
|
03 (март)
| dd |
ddd |
| 01 |
060 |
| 02 |
061 |
| 03 |
062 |
| 04 |
063 |
| 05 |
064 |
| 06 |
065 |
| 07 |
066 |
| 08 |
067 |
| 09 |
068 |
| 10 |
069 |
| 11 |
070 |
| 12 |
071 |
| 13 |
072 |
| 14 |
073 |
| 15 |
074 |
| 16 |
075 |
| 17 |
076 |
| 18 |
077 |
| 19 |
078 |
| 20 |
079 |
| 21 |
080 |
| 22 |
081 |
| 23 |
082 |
| 24 |
083 |
| 25 |
084 |
| 26 |
085 |
| 27 |
086 |
| 28 |
087 |
| 29 |
088 |
| 30 |
089 |
| 31 |
090 |
|
04 (апр.)
| dd |
ddd |
| 01 |
091 |
| 02 |
092 |
| 03 |
093 |
| 04 |
094 |
| 05 |
095 |
| 06 |
096 |
| 07 |
097 |
| 08 |
098 |
| 09 |
099 |
| 10 |
100 |
| 11 |
101 |
| 12 |
102 |
| 13 |
103 |
| 14 |
104 |
| 15 |
105 |
| 16 |
106 |
| 17 |
107 |
| 18 |
108 |
| 19 |
109 |
| 20 |
110 |
| 21 |
111 |
| 22 |
112 |
| 23 |
113 |
| 24 |
114 |
| 25 |
115 |
| 26 |
116 |
| 27 |
117 |
| 28 |
118 |
| 29 |
119 |
| 30 |
120 |
|
05 (май)
| dd |
ddd |
| 01 |
121 |
| 02 |
122 |
| 03 |
123 |
| 04 |
124 |
| 05 |
125 |
| 06 |
126 |
| 07 |
127 |
| 08 |
128 |
| 09 |
129 |
| 10 |
130 |
| 11 |
131 |
| 12 |
132 |
| 13 |
133 |
| 14 |
134 |
| 15 |
135 |
| 16 |
136 |
| 17 |
137 |
| 18 |
138 |
| 19 |
139 |
| 20 |
140 |
| 21 |
141 |
| 22 |
142 |
| 23 |
143 |
| 24 |
144 |
| 25 |
145 |
| 26 |
146 |
| 27 |
147 |
| 28 |
148 |
| 29 |
149 |
| 30 |
150 |
| 31 |
151 |
|
06 (июнь)
| dd |
ddd |
| 01 |
152 |
| 02 |
153 |
| 03 |
154 |
| 04 |
155 |
| 05 |
156 |
| 06 |
157 |
| 07 |
158 |
| 08 |
159 |
| 09 |
160 |
| 10 |
161 |
| 11 |
162 |
| 12 |
163 |
| 13 |
164 |
| 14 |
165 |
| 15 |
166 |
| 16 |
167 |
| 17 |
168 |
| 18 |
169 |
| 19 |
170 |
| 20 |
171 |
| 21 |
172 |
| 22 |
173 |
| 23 |
174 |
| 24 |
175 |
| 25 |
176 |
| 26 |
177 |
| 27 |
178 |
| 28 |
179 |
| 29 |
180 |
| 30 |
181 |
|
07 (июль)
| dd |
ddd |
| 01 |
182 |
| 02 |
183 |
| 03 |
184 |
| 04 |
185 |
| 05 |
186 |
| 06 |
187 |
| 07 |
188 |
| 08 |
189 |
| 09 |
190 |
| 10 |
191 |
| 11 |
192 |
| 12 |
193 |
| 13 |
194 |
| 14 |
195 |
| 15 |
196 |
| 16 |
197 |
| 17 |
198 |
| 18 |
199 |
| 19 |
200 |
| 20 |
201 |
| 21 |
202 |
| 22 |
203 |
| 23 |
204 |
| 24 |
205 |
| 25 |
206 |
| 26 |
207 |
| 27 |
208 |
| 28 |
209 |
| 29 |
210 |
| 30 |
211 |
| 31 |
212 |
|
08 (авг.)
| dd |
ddd |
| 01 |
213 |
| 02 |
214 |
| 03 |
215 |
| 04 |
216 |
| 05 |
217 |
| 06 |
218 |
| 07 |
219 |
| 08 |
220 |
| 09 |
221 |
| 10 |
222 |
| 11 |
223 |
| 12 |
224 |
| 13 |
225 |
| 14 |
226 |
| 15 |
227 |
| 16 |
228 |
| 17 |
229 |
| 18 |
230 |
| 19 |
231 |
| 20 |
232 |
| 21 |
233 |
| 22 |
234 |
| 23 |
235 |
| 24 |
236 |
| 25 |
237 |
| 26 |
238 |
| 27 |
239 |
| 28 |
240 |
| 29 |
241 |
| 30 |
242 |
| 31 |
243 |
|
09 (сен.)
| dd |
ddd |
| 01 |
244 |
| 02 |
245 |
| 03 |
246 |
| 04 |
247 |
| 05 |
248 |
| 06 |
249 |
| 07 |
250 |
| 08 |
251 |
| 09 |
252 |
| 10 |
253 |
| 11 |
254 |
| 12 |
255 |
| 13 |
256 |
| 14 |
257 |
| 15 |
258 |
| 16 |
259 |
| 17 |
260 |
| 18 |
261 |
| 19 |
262 |
| 20 |
263 |
| 21 |
264 |
| 22 |
265 |
| 23 |
266 |
| 24 |
267 |
| 25 |
268 |
| 26 |
269 |
| 27 |
270 |
| 28 |
271 |
| 29 |
272 |
| 30 |
273 |
|
10 (окт.)
| dd |
ddd |
| 01 |
274 |
| 02 |
275 |
| 03 |
276 |
| 04 |
277 |
| 05 |
278 |
| 06 |
279 |
| 07 |
280 |
| 08 |
281 |
| 09 |
282 |
| 10 |
283 |
| 11 |
284 |
| 12 |
285 |
| 13 |
286 |
| 14 |
287 |
| 15 |
288 |
| 16 |
289 |
| 17 |
290 |
| 18 |
291 |
| 19 |
292 |
| 20 |
293 |
| 21 |
294 |
| 22 |
295 |
| 23 |
296 |
| 24 |
297 |
| 25 |
298 |
| 26 |
299 |
| 27 |
300 |
| 28 |
301 |
| 29 |
302 |
| 30 |
303 |
| 31 |
304 |
|
11 (ноя.)
| dd |
ddd |
| 01 |
305 |
| 02 |
306 |
| 03 |
307 |
| 04 |
308 |
| 05 |
309 |
| 06 |
310 |
| 07 |
311 |
| 08 |
312 |
| 09 |
313 |
| 10 |
314 |
| 11 |
315 |
| 12 |
316 |
| 13 |
317 |
| 14 |
318 |
| 15 |
319 |
| 16 |
320 |
| 17 |
321 |
| 18 |
322 |
| 19 |
323 |
| 20 |
324 |
| 21 |
325 |
| 22 |
326 |
| 23 |
327 |
| 24 |
328 |
| 25 |
329 |
| 26 |
330 |
| 27 |
331 |
| 28 |
332 |
| 29 |
333 |
| 30 |
334 |
|
12 (дек.)
| dd |
ddd |
| 01 |
335 |
| 02 |
336 |
| 03 |
337 |
| 04 |
338 |
| 05 |
339 |
| 06 |
340 |
| 07 |
341 |
| 08 |
342 |
| 09 |
343 |
| 10 |
344 |
| 11 |
345 |
| 12 |
346 |
| 13 |
347 |
| 14 |
348 |
| 15 |
349 |
| 16 |
350 |
| 17 |
351 |
| 18 |
352 |
| 19 |
353 |
| 20 |
354 |
| 21 |
355 |
| 22 |
356 |
| 23 |
357 |
| 24 |
358 |
| 25 |
359 |
| 26 |
360 |
| 27 |
361 |
| 28 |
362 |
| 29 |
363 |
| 30 |
364 |
| 31 |
365 |
|
|
Соответствие обычных и упрощённых дат для ВК
Для простых годов в период (включительно):
dd мес.yyyy от 01 сен.yyyy по 28 фев.yyyy
ddd.yyyy от 001.yyyy по 181.yyyy |
сентябрь
| dd |
ddd |
| 01 |
001 |
| 02 |
002 |
| 03 |
003 |
| 04 |
004 |
| 05 |
005 |
| 06 |
006 |
| 07 |
007 |
| 08 |
008 |
| 09 |
009 |
| 10 |
010 |
| 11 |
011 |
| 12 |
012 |
| 13 |
013 |
| 14 |
014 |
| 15 |
015 |
|
| dd |
ddd |
| 16 |
016 |
| 17 |
017 |
| 18 |
018 |
| 19 |
019 |
| 20 |
020 |
| 21 |
021 |
| 22 |
022 |
| 23 |
023 |
| 24 |
024 |
| 25 |
025 |
| 26 |
026 |
| 27 |
027 |
| 28 |
028 |
| 29 |
029 |
| 30 |
030 |
|
|
октябрь
| dd |
ddd |
| 01 |
031 |
| 02 |
032 |
| 03 |
033 |
| 04 |
034 |
| 05 |
035 |
| 06 |
036 |
| 07 |
037 |
| 08 |
038 |
| 09 |
039 |
| 10 |
040 |
| 11 |
041 |
| 12 |
042 |
| 13 |
043 |
| 14 |
044 |
| 15 |
045 |
|
| dd |
ddd |
| 16 |
046 |
| 17 |
047 |
| 18 |
048 |
| 19 |
049 |
| 20 |
050 |
| 21 |
051 |
| 22 |
052 |
| 23 |
053 |
| 24 |
054 |
| 25 |
055 |
| 26 |
056 |
| 27 |
057 |
| 28 |
058 |
| 29 |
059 |
| 30 |
060 |
| 31 |
061 |
|
|
ноябрь
| dd |
ddd |
| 01 |
062 |
| 02 |
063 |
| 03 |
064 |
| 04 |
065 |
| 05 |
066 |
| 06 |
067 |
| 07 |
068 |
| 08 |
069 |
| 09 |
070 |
| 10 |
071 |
| 11 |
072 |
| 12 |
073 |
| 13 |
074 |
| 14 |
075 |
| 15 |
076 |
|
| dd |
ddd |
| 16 |
077 |
| 17 |
078 |
| 18 |
079 |
| 19 |
080 |
| 20 |
081 |
| 21 |
082 |
| 22 |
083 |
| 23 |
084 |
| 24 |
085 |
| 25 |
086 |
| 26 |
087 |
| 27 |
088 |
| 28 |
089 |
| 29 |
090 |
| 30 |
091 |
|
|
декабрь
| dd |
ddd |
| 01 |
092 |
| 02 |
093 |
| 03 |
094 |
| 04 |
095 |
| 05 |
096 |
| 06 |
097 |
| 07 |
098 |
| 08 |
099 |
| 09 |
100 |
| 10 |
101 |
| 11 |
102 |
| 12 |
103 |
| 13 |
104 |
| 14 |
105 |
| 15 |
106 |
|
| dd |
ddd |
| 16 |
107 |
| 17 |
108 |
| 18 |
109 |
| 19 |
110 |
| 20 |
111 |
| 21 |
112 |
| 22 |
113 |
| 23 |
114 |
| 24 |
115 |
| 25 |
116 |
| 26 |
117 |
| 27 |
118 |
| 28 |
119 |
| 29 |
120 |
| 30 |
121 |
| 31 |
122 |
|
|
январь
| dd |
ddd |
| 01 |
123 |
| 02 |
124 |
| 03 |
125 |
| 04 |
126 |
| 05 |
127 |
| 06 |
128 |
| 07 |
129 |
| 08 |
130 |
| 09 |
131 |
| 10 |
132 |
| 11 |
133 |
| 12 |
134 |
| 13 |
135 |
| 14 |
136 |
| 15 |
137 |
|
| dd |
ddd |
| 16 |
138 |
| 17 |
139 |
| 18 |
140 |
| 19 |
141 |
| 20 |
142 |
| 21 |
143 |
| 22 |
144 |
| 23 |
145 |
| 24 |
146 |
| 25 |
147 |
| 26 |
148 |
| 27 |
149 |
| 28 |
150 |
| 29 |
151 |
| 30 |
152 |
| 31 |
153 |
|
|
февраль
| dd |
ddd |
| 01 |
154 |
| 02 |
155 |
| 03 |
156 |
| 04 |
157 |
| 05 |
158 |
| 06 |
159 |
| 07 |
160 |
| 08 |
161 |
| 09 |
162 |
| 10 |
163 |
| 11 |
164 |
| 12 |
165 |
| 13 |
166 |
| 14 |
167 |
| 15 |
168 |
|
| dd |
ddd |
| 16 |
169 |
| 17 |
170 |
| 18 |
171 |
| 19 |
172 |
| 20 |
173 |
| 21 |
174 |
| 22 |
175 |
| 23 |
176 |
| 24 |
177 |
| 25 |
178 |
| 26 |
179 |
| 27 |
180 |
| 28 |
181 |
|
|
|
Для високосных годов в период (включительно):
dd мес.yyyy от 01 сен.yyyy по 29 фев.yyyy
ddd.yyyy от 000.yyyy по 181.yyyy |
сентябрь
| dd |
ddd |
| 01 |
000 |
| 02 |
001 |
| 03 |
002 |
| 04 |
003 |
| 05 |
004 |
| 06 |
005 |
| 07 |
006 |
| 08 |
007 |
| 09 |
008 |
| 10 |
009 |
| 11 |
010 |
| 12 |
011 |
| 13 |
012 |
| 14 |
013 |
| 15 |
014 |
|
| dd |
ddd |
| 16 |
015 |
| 17 |
016 |
| 18 |
017 |
| 19 |
018 |
| 20 |
019 |
| 21 |
020 |
| 22 |
021 |
| 23 |
022 |
| 24 |
023 |
| 25 |
024 |
| 26 |
025 |
| 27 |
026 |
| 28 |
027 |
| 29 |
028 |
| 30 |
029 |
|
|
октябрь
| dd |
ddd |
| 01 |
030 |
| 02 |
031 |
| 03 |
032 |
| 04 |
033 |
| 05 |
034 |
| 06 |
035 |
| 07 |
036 |
| 08 |
037 |
| 09 |
038 |
| 10 |
039 |
| 11 |
040 |
| 12 |
041 |
| 13 |
042 |
| 14 |
043 |
| 15 |
044 |
|
| dd |
ddd |
| 16 |
045 |
| 17 |
046 |
| 18 |
047 |
| 19 |
048 |
| 20 |
049 |
| 21 |
050 |
| 22 |
051 |
| 23 |
052 |
| 24 |
053 |
| 25 |
054 |
| 26 |
055 |
| 27 |
056 |
| 28 |
057 |
| 29 |
058 |
| 30 |
059 |
| 31 |
060 |
|
|
ноябрь
| dd |
ddd |
| 01 |
061 |
| 02 |
062 |
| 03 |
063 |
| 04 |
064 |
| 05 |
065 |
| 06 |
066 |
| 07 |
067 |
| 08 |
068 |
| 09 |
069 |
| 10 |
070 |
| 11 |
071 |
| 12 |
072 |
| 13 |
073 |
| 14 |
074 |
| 15 |
075 |
|
| dd |
ddd |
| 16 |
076 |
| 17 |
077 |
| 18 |
078 |
| 19 |
079 |
| 20 |
080 |
| 21 |
081 |
| 22 |
082 |
| 23 |
083 |
| 24 |
084 |
| 25 |
085 |
| 26 |
086 |
| 27 |
087 |
| 28 |
088 |
| 29 |
089 |
| 30 |
090 |
|
|
декабрь
| dd |
ddd |
| 01 |
091 |
| 02 |
092 |
| 03 |
093 |
| 04 |
094 |
| 05 |
095 |
| 06 |
096 |
| 07 |
097 |
| 08 |
098 |
| 09 |
099 |
| 10 |
100 |
| 11 |
101 |
| 12 |
102 |
| 13 |
103 |
| 14 |
104 |
| 15 |
105 |
|
| dd |
ddd |
| 16 |
106 |
| 17 |
107 |
| 18 |
108 |
| 19 |
109 |
| 20 |
110 |
| 21 |
111 |
| 22 |
112 |
| 23 |
113 |
| 24 |
114 |
| 25 |
115 |
| 26 |
116 |
| 27 |
117 |
| 28 |
118 |
| 29 |
119 |
| 30 |
120 |
| 31 |
121 |
|
|
январь
| dd |
ddd |
| 01 |
122 |
| 02 |
123 |
| 03 |
124 |
| 04 |
125 |
| 05 |
126 |
| 06 |
127 |
| 07 |
128 |
| 08 |
129 |
| 09 |
130 |
| 10 |
131 |
| 11 |
132 |
| 12 |
133 |
| 13 |
134 |
| 14 |
135 |
| 15 |
136 |
|
| dd |
ddd |
| 16 |
137 |
| 17 |
138 |
| 18 |
139 |
| 19 |
140 |
| 20 |
141 |
| 21 |
142 |
| 22 |
143 |
| 23 |
144 |
| 24 |
145 |
| 25 |
146 |
| 26 |
147 |
| 27 |
148 |
| 28 |
149 |
| 29 |
150 |
| 30 |
151 |
| 31 |
152 |
|
|
февраль
| dd |
ddd |
| 01 |
153 |
| 02 |
154 |
| 03 |
155 |
| 04 |
156 |
| 05 |
157 |
| 06 |
158 |
| 07 |
159 |
| 08 |
160 |
| 09 |
161 |
| 10 |
162 |
| 11 |
163 |
| 12 |
164 |
| 13 |
165 |
| 14 |
166 |
| 15 |
167 |
|
| dd |
ddd |
| 16 |
168 |
| 17 |
169 |
| 18 |
170 |
| 19 |
171 |
| 20 |
172 |
| 21 |
173 |
| 22 |
174 |
| 23 |
175 |
| 24 |
176 |
| 25 |
177 |
| 26 |
178 |
| 27 |
179 |
| 28 |
180 |
| 29 |
181 |
|
|
|
Для любых годов в период (включительно):
dd мес.yyyy от 01 мар.yyyy по 31 авг.yyyy
ddd.yyyy от 182.yyyy по 365.yyyy |
март
| dd |
ddd |
| 01 |
182 |
| 02 |
183 |
| 03 |
184 |
| 04 |
185 |
| 05 |
186 |
| 06 |
187 |
| 07 |
188 |
| 08 |
189 |
| 09 |
190 |
| 10 |
191 |
| 11 |
192 |
| 12 |
193 |
| 13 |
194 |
| 14 |
195 |
| 15 |
196 |
|
| dd |
ddd |
| 16 |
197 |
| 17 |
198 |
| 18 |
199 |
| 19 |
200 |
| 20 |
201 |
| 21 |
202 |
| 22 |
203 |
| 23 |
204 |
| 24 |
205 |
| 25 |
206 |
| 26 |
207 |
| 27 |
208 |
| 28 |
209 |
| 29 |
210 |
| 30 |
211 |
| 31 |
212 |
|
|
апрель
| dd |
ddd |
| 01 |
213 |
| 02 |
214 |
| 03 |
215 |
| 04 |
216 |
| 05 |
217 |
| 06 |
218 |
| 07 |
219 |
| 08 |
220 |
| 09 |
221 |
| 10 |
222 |
| 11 |
223 |
| 12 |
224 |
| 13 |
225 |
| 14 |
226 |
| 15 |
227 |
|
| dd |
ddd |
| 16 |
228 |
| 17 |
229 |
| 18 |
230 |
| 19 |
231 |
| 20 |
232 |
| 21 |
233 |
| 22 |
234 |
| 23 |
235 |
| 24 |
236 |
| 25 |
237 |
| 26 |
238 |
| 27 |
239 |
| 28 |
240 |
| 29 |
241 |
| 30 |
242 |
|
|
май
| dd |
ddd |
| 01 |
243 |
| 02 |
244 |
| 03 |
245 |
| 04 |
246 |
| 05 |
247 |
| 06 |
248 |
| 07 |
249 |
| 08 |
250 |
| 09 |
251 |
| 10 |
252 |
| 11 |
253 |
| 12 |
254 |
| 13 |
255 |
| 14 |
256 |
| 15 |
257 |
|
| dd |
ddd |
| 16 |
258 |
| 17 |
259 |
| 18 |
260 |
| 19 |
261 |
| 20 |
262 |
| 21 |
263 |
| 22 |
264 |
| 23 |
265 |
| 24 |
266 |
| 25 |
267 |
| 26 |
268 |
| 27 |
269 |
| 28 |
270 |
| 29 |
271 |
| 30 |
272 |
| 31 |
273 |
|
|
июнь
| dd |
ddd |
| 01 |
274 |
| 02 |
275 |
| 03 |
276 |
| 04 |
277 |
| 05 |
278 |
| 06 |
279 |
| 07 |
280 |
| 08 |
281 |
| 09 |
282 |
| 10 |
283 |
| 11 |
284 |
| 12 |
285 |
| 13 |
286 |
| 14 |
287 |
| 15 |
288 |
|
| dd |
ddd |
| 16 |
289 |
| 17 |
290 |
| 18 |
291 |
| 19 |
292 |
| 20 |
293 |
| 21 |
294 |
| 22 |
295 |
| 23 |
296 |
| 24 |
297 |
| 25 |
298 |
| 26 |
299 |
| 27 |
300 |
| 28 |
301 |
| 29 |
302 |
| 30 |
303 |
|
|
июль
| dd |
ddd |
| 01 |
304 |
| 02 |
305 |
| 03 |
306 |
| 04 |
307 |
| 05 |
308 |
| 06 |
309 |
| 07 |
310 |
| 08 |
311 |
| 09 |
312 |
| 10 |
313 |
| 11 |
314 |
| 12 |
315 |
| 13 |
316 |
| 14 |
317 |
| 15 |
318 |
|
| dd |
ddd |
| 16 |
319 |
| 17 |
320 |
| 18 |
321 |
| 19 |
322 |
| 20 |
323 |
| 21 |
324 |
| 22 |
325 |
| 23 |
326 |
| 24 |
327 |
| 25 |
328 |
| 26 |
329 |
| 27 |
330 |
| 28 |
331 |
| 29 |
332 |
| 30 |
333 |
| 31 |
334 |
|
|
август
| dd |
ddd |
| 01 |
335 |
| 02 |
336 |
| 03 |
337 |
| 04 |
338 |
| 05 |
339 |
| 06 |
340 |
| 07 |
341 |
| 08 |
342 |
| 09 |
343 |
| 10 |
344 |
| 11 |
345 |
| 12 |
346 |
| 13 |
347 |
| 14 |
348 |
| 15 |
349 |
|
| dd |
ddd |
| 16 |
350 |
| 17 |
351 |
| 18 |
352 |
| 19 |
353 |
| 20 |
354 |
| 21 |
355 |
| 22 |
356 |
| 23 |
357 |
| 24 |
358 |
| 25 |
359 |
| 26 |
360 |
| 27 |
361 |
| 28 |
362 |
| 29 |
363 |
| 30 |
364 |
| 31 |
365 |
|
|
|