«Наука и жизнь» № 8, 2000 г., стр. 83 – 87
http://www.nkj.ru/archive/articles/8028/

БЕСЕДЫ ОБ ОСНОВАХ НАУК

ЧЕРНЫЕ ДЫРЫ ВО ВСЕЛЕННОЙ

С. Транковский

Среди наиболее важных и интересных проблем современной физики и астрофизики академик В. Л. Гинзбург назвал вопросы, связанные с черными дырами (см. «Наука и жизнь» №№ 11, 12, 1999 г.* ). Существование этих странных объектов было предсказано более двухсот лет назад, условия, приводящие к их образованию, точно рассчитали в конце 30‑х годов XX века, а вплотную астрофизика занялась ими менее сорока лет назад. Сегодня научные журналы мира ежегодно публикуют тысячи статей, посвященных черным дырам.

КАК ОНИ ВОЗНИКАЮТ

В 1783 году английский математик Джон Митчел, а спустя тринадцать лет независимо от него французский астроном и математик Пьер Симон Лаплас провели очень странное исследование. Они рассмотрели условия, при которых свет не сможет покинуть звезду.

Логика ученых была проста. Для любого астрономического объекта (планеты или звезды) можно вычислить так называемую скорость убегания, или вторую космическую скорость, позволяющую любому телу или частице навсегда его покинуть. А в физике того времени безраздельно господствовала ньютоновская теория, согласно которой свет – это поток частиц (до теории электромагнитных волн и квантов оставалось еще почти полтораста лет). Скорость убегания частиц можно рассчитать исходя из равенства потенциальной энергии на поверхности планеты и кинетической энергии тела, «убежавшего» на бескончно большое расстояние. Эта скорость определяется формулой

где M – масса космического объекта, R – его радиус, G – гравитационная постоянная.

Отсюда легко получается радиус тела заданной массы (позднее получивший название «гравитационный радиус r_g »), при котором скорость убегания равна скорости света:

Это значит, что звезда, сжатая в сферу радиусом r_g< 2GM / c ², перестанет излучать – свет покинуть ее не сможет. Во Вселенной возникнет черная дыра.

Несложно рассчитать, что Солнце (его масса 2 ·10 ³³ г) превратится в черную дыру, если сожмется до радиуса примерно 3 километра. Плотность его вещества при этом достигнет 10 ¹⁶ г/см ³. Радиус Земли, сжатой до состояния черной дыры, уменьшился бы примерно до одного сантиметра.

Казалось невероятным, что в природе могут найтись силы, способные сжать звезду до столь ничтожных размеров. Поэтому выводы из работ Митчела и Лапласа более ста лет считались чем-то вроде математического парадокса, не имеющего физического смысла.

Строгое математическое доказательство того, что подобный экзотический объект в космосе возможен, было получено только в 1916 году. Немецкий астроном Карл Шварцшильд, проведя анализ уравнений общей теории относительности Альберта Эйнштейна, получил интересный результат. Исследовав движение частицы в гравитационном поле массивного тела, он пришел к выводу: уравнение теряет физический смысл (его решение обращается в бесконечность) при r = 0 и r = r_g.

Точки, в которых характеристики поля теряют смысл, называются сингулярными, то есть особыми. Сингулярность в нулевой точке отражает точечную, или, что то же самое, центрально-симметричную структуру поля (ведь любое сферическое тело – звезду или планету – можно представить как материальную точку). А точки, расположенные на сферической поверхности радиусом r_g, образуют ту самую поверхность, с которой скорость убегания равна скорости света. В общей теории относительности она именуется сингулярной сферой Шварцшильда или горизонтом событий (почему – станет ясно в дальнейшем).

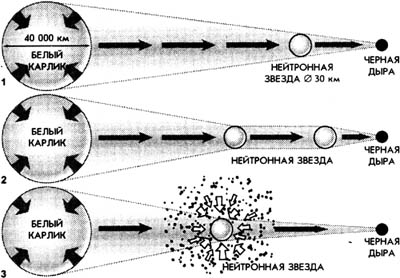
Образование черной дыры может происходить тремя путями. Звезда, масса которой превышает две-три массы Солнца, в конце своей жизни сжимается в белый карлик. Если его масса велика, сжатие продолжается и белый карлик превращается в нейтронную звезду, которая коллапсирует до черной дыры либо сразу (1), либо после остывания (2). Массы нейтронной звезды может не хватить для коллапса, и тогда он начнется после того, как звезда всосет в себя достаточное количество межзвездного вещества (3).

Уже на примере знакомых нам объектов – Земли и Солнца – ясно, что черные дыры представляют собой весьма странные объекты. Даже астрономы, имеющие дело с веществом при экстремальных значениях температуры, плотности и давления, считают их весьма экзотическими, и до последнего времени далеко не все верили в их существование. Однако первые указания на возможность образования черных дыр содержались уже в общей теории относительности А. Эйнштейна, созданной в 1915 году. Английский астроном Артур Эддингтон, один из первых интерпретаторов и популяризаторов теории относительности, в 30-х годах вывел систему уравнений, описывающих внутреннее строение звезд. Из них следует, что звезда находится в равновесии под действием противоположно направленных сил тяготения и внутреннего давления, создаваемого движением частиц горячей плазмы внутри светила и напором излучения, образующегося в его недрах. А это означает, что звезда представляет собой газовый шар, в центре которого высокая температура, постепенно понижающаяся к периферии. Из уравнений, в частности, следовало, что температура поверхности Солнца составляет около 5500 градусов (что вполне соответствовало данным астрономических измерений), а в его центре должна быть порядка 10 миллионов градусов. Это позволило Эддингтону сделать пророческий вывод: при такой температуре «зажигается» термоядерная реакция, достаточная для обеспечения свечения Солнца. Физики-атомщики того времени с этим не соглашались. Им казалось, что в недрах звезды слишком «холодно»: температура там недостаточна, чтобы реакция «пошла». На это взбешенный теоретик отвечал: «Поищите местечко погорячее!».

И в конечном итоге он оказался прав: в центре звезды действительно идет термоядерная реакция (другое дело, что так называемая «стандартная солнечная модель», основанная на представлениях о термоядерном синтезе, по-видимому, оказалась неверной – см., например, «Наука и жизнь» №№ 2, 3, 2000 г.). Но тем не менее реакция в центре звезды проходит, звезда светит, а излучение, которое при этом возникает, удерживает ее в стабильном состоянии. Но вот ядерное «горючее» в звезде выгорает. Выделение энергии прекращается, излучение гаснет, и сила, сдерживающая гравитационное притяжение, исчезает. Существует ограничение на массу звезды, после которого звезда начинает необратимо сжиматься. Расчеты показывают, что это происходит, если масса звезды превышает две-три массы Солнца.

ГРАВИТАЦИОННЫЙ КОЛЛАПС

Вначале скорость сжатия звезды невелика, но его темп непрерывно возрастает, поскольку сила притяжения обратно пропорциональна квадрату расстояния. Сжатие становится необратимым, сил, способных противодействовать самогравитации, нет. Такой процесс называется гравитационным коллапсом. Скорость движения оболочки звезды к ее центру увеличивается, приближаясь к скорости света. И здесь начинают играть роль эффекты теории относительности.

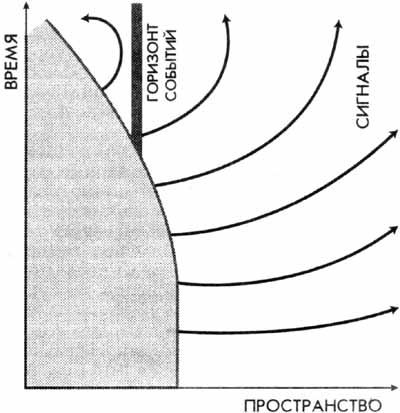
Так принято изображать процессы, идущие в окрестностях коллапсирующей черной дыры. С течением времени (Y) пространство (X) вокруг нее (закрашенная область) сжимается, устремляясь к сингулярности. Сигналы (2), идущие с ее поверхности, достигают наблюдателя за все большие промежутки времени – возникает гравитационное красное смещение. Когда радиус черной дыры становится меньше шварцшильдовского, сигналы приходить перестают. Со стороны кажется, что время остановилось.

Скорость убегания была рассчитана исходя из ньютоновсих представлений о природе света. С точки зрения общей теории относительности явления в окрестностях коллапсирующей звезды происходят несколько по-другому. В ее мощном поле тяготения возникает так называемое гравитационное красное смещение. Это означает, что частота излучения, исходящего от массивного объекта, смещается в сторону низких частот. В пределе, на границе сферы Шварцшильда, частота излучения становится равной нулю. То есть наблюдатель, находящийся за ее пределами, ничего не сможет узнать о том, что происходит внутри. Именно поэтому сферу Шварцшильда и называют горизонтом событий.

Но уменьшение частоты равнозначно замедлению времени, и, когда частота становится равна нулю, время останавливается. Это означает, что посторонний наблюдатель увидит очень странную картину: оболочка звезды, падающая с нарастающим ускорением, вместо того, чтобы достигнуть скорости света, останавливается. С его точки зрения, сжатие прекратится, как только размеры звезды приблизятся к гравитационному радиусу. Он никогда не увидит, чтобы хоть одна частица «нырнула» под сферу Шварцшильда. Но для гипотетического наблюдателя, падающего на черную дыру, все закончится в считанные мгновения по его часам. Так, время гравитационного коллапса звезды размером с Солнце составит 29 минут, а гораздо более плотной и компактной нейтронной звезды – только 1/20000 секунды. И здесь его подстерегает неприятность, связанная с геометрией пространства-времени вблизи черной дыры.

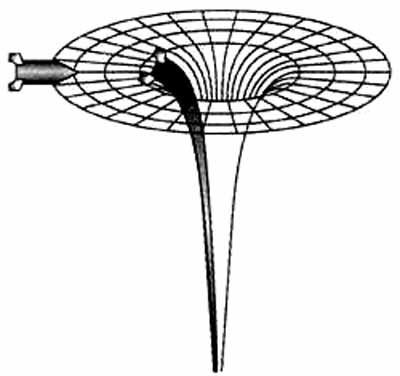
Гравитационное поле черной дыры вносит сильнейшие искажения в геометрию пространства. На большом расстоянии пространство можно считаь плоским, евклидовым. Но по мере приближения к черной дыре оно все сильнее деформируется, и аналогичным образом изменяется форма предмета, падающего в черную дыру. Сторонний наблюдатель увидит, что предмет растягивается в бесконечно тонкую нить бесконечной длины. Наблюдатель же, падающий на черную дыру, ничего при этом не заметит.

Наблюдатель попадает в искривленное пространство. Вблизи гравитационного радиуса силы тяготения становятся бесконечно большими; они растягивают ракету с космонавтом-наблюдателем в бесконечно тонкую нить бесконечной длины. Но сам он этого не заметит: все его деформации будут соответствовать искажениям пространственно-временных координат. Эти рассуждения, конечно, относятся к идеальному, гипотетическому случаю. Любое реальное тело будет разорвано приливными силами задолго до подхода к сфере Шварцшильда.

РАЗМЕРЫ ЧЕРНЫХ ДЫР

Размер черной дыры, а точнее – радиус сферы Шварцшильда пропорционален массе звезды. А поскольку астрофизика никаких ограничений на размер звезды не накладывает, то и черная дыра может быть сколь угодно велика. Если она, например, возникла при коллапсе звезды массой 10 ⁸ масс Солнца (или за счет слияния сотен тысяч, а то и миллионов сравнительно небольших звезд), ее радиус будет около 300 миллионов километров, вдвое больше земной орбиты. А средняя плотность вещества такого гиганта близка к плотности воды.

По-видимому, именно такие черные дыры находятся в центрах галактик. Во всяком случае, астрономы сегодня насчитывают около пятидесяти галактик, в центре которых, судя по косвенным признакам (речь о них пойдет ниже), имеются черные дыры массой порядка миллиарда (10 ⁹) солнечной. В нашей Галактике тоже, видимо, есть своя черная дыра; ее массу удалось оценить довольно точно – 2,4 ·10 ⁶ ± 10% массы Солнца.

Теория предполагает, что наряду с такими сверхгигантами должны были возникать и черные мини-дыры массой порядка 10 ¹⁴ г и радиусом порядка 10 ^– 12 см (размер атомного ядра). Они могли появляться в первые мгновения существования Вселенной как проявление очень сильной неоднородности пространства-времени при колоссальной плотности энергии. Условия, которые были тогда во Вселенной, исследователи сегодня реализуют на мощных коллайдерах (ускорителях на встречных пучках). Эксперименты в ЦЕРНе, проведенные в начале этого года, позволили получить кварк-глюонную плазму – материю, существовавшую до возникновения элементарных частиц. Исследования этого состояния вещества продолжаются в Брукхевене – американском ускорительном центре. Он способен разогнать частицы до энергий, на полтора-два порядка более высоких, чем ускоритель в ЦЕРНе. Готовящийся эксперимент вызвал нешуточную тревогу: не возникнет ли при его проведении черная мини-дыра, которая искривит наше пространство и погубит Землю?

Это опасение вызвало столь сильный резонанс, что правительство США было вынуждено созвать авторитетную комиссию для проверки такой возможности. Комиссия, состоявшая из видных исследователей, дала заключение: энергия ускорителя слишком мала, чтобы черная дыра могла возникнуть (об этом эксперименте рассказано в журнале «Наука и жизнь» № 3, 2000 г.).

КАК УВИДЕТЬ НЕВИДИМОЕ

Черные дыры ничего не излучают, даже свет. Однако астрономы научились видеть их, вернее – находить «кандидатов» на эту роль. Есть три способа обнаружить черную дыру.

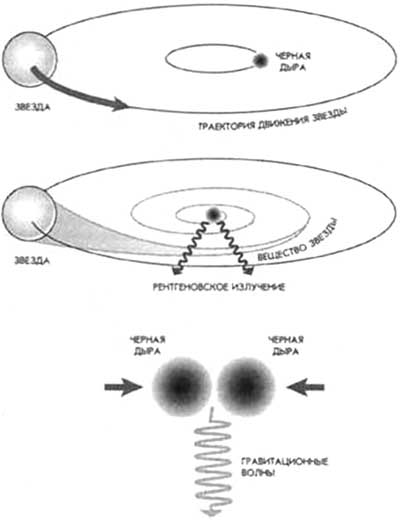
1. Нужно проследить за обращением звезд в скоплениях вокруг некоего центра гравитации. Если окажется, что в этом центре ничего нет, и звезды крутятся как бы вокруг пустого места, можно достаточно уверенно сказать: в этой «пустоте» находится черная дыра. Именно по этому признаку предположили наличие черной дыры в центре нашей Галактики и оценили ее массу.

2. Черная дыра активно всасывает в себя материю из окружающего пространства. Межзвездная пыль, газ, вещество ближайших звезд падают на нее по спирали, образуя так называемый аккреционный диск, подобный кольцу Сатурна. (Именно это и пугало в брукхевенском эксперименте: черная мини-дыра, возникшая в ускорителе, начнет всасывать в себя Землю, причем процесс этот никакими силами остановить было бы нельзя.) Приближаясь к сфере Шварцшильда, частицы испытывают ускорение и начинают излучать в рентгеновском диапазоне. Это излучение имеет характерный спектр, подобный хорошо изученному излучению частиц, ускоренных в синхротроне. И если из какой-то области Вселенной приходит такое излучение, можно с уверенностью сказать – там должна быть черная дыра.

3. При слиянии двух черных дыр возникает гравитационное излучение. Подсчитано, что если масса каждой составляет около десяти масс Солнца, то при их слиянии за считанные часы в виде гравитационных волн выделится энергия, эквивалентная 1 % их суммарной массы. Это в тысячу раз больше той световой, тепловой и прочей энергии, которую излучило Солнце за все время своего существования – пять миллиардов лет. Обнаружить гравитационное излучение надеются с помощью гравитационно-волновых обсерваторий LIGO и других, которые строятся сейчас в Америке и Европе при участии российских исследователей (см. «Наука и жизнь» № 5, 2000 г.** ).

Черная дыра, невидимая в телескоп, обнаруживает себя только по своему гравитационному воздействию. Она заставляет звезды двигаться по эллиптическим траекториям вокруг якобы пустого места, втягивает в себя вещество звезд и космическую пыль. При слиянии двух черных дыр возникает мощнейший всплеск гравитационного излучения.

И все-таки, хотя у астрономов нет никаких сомнений в существовании черных дыр, категорически утверждать, что в данной точке пространства находится именно одна из них, никто не берется. Научная этика, добросовестность исследователя требуют получить на поставленный вопрос ответ однозначный, не терпящий разночтений. Мало оценить массу невидимого объекта, нужно измерить его радиус и показать, что он не превышает шварцшильдовский. А даже в пределах нашей Галактики эта задача пока неразрешима. Именно поэтому ученые проявляют известную сдержанность в сообщениях об их обнаружении, а научные журналы буквально набиты сообщениями о теоретических работах и наблюдениях эффектов, способных пролить свет на их загадку.

Есть, правда, у черных дыр и еще одно свойство, предсказанное теоретически, которое, возможно, позволило бы увидеть их. Но, правда, при одном условии: масса черной дыры должна быть гораздо меньше массы Солнца.

ЧЕРНАЯ ДЫРА МОЖЕТ БЫТЬ И «БЕЛОЙ»

Долгое время черные дыры считались воплощением тьмы, объектами, которые в вакууме, в отсутствии поглощения материи, ничего не излучают. Однако в 1974 году известный английский теоретик Стивен Хокинг показал, что черным дырам можно приписать температуру, и, следовательно, они должны излучать.

Согласно представлениям квантовой механики, вакуум – не пустота, а некая «пена пространства-времени», мешанина из виртуалных (ненаблюдаемых в нашем мире) частиц. Однако квантовые флуктуации энергии способны «выбросить» из вакуума пару частица-античастица. Например, при столкновении двух-трех гамма-квантов как бы из ничего возникнут электрон и позитрон. Это и аналогичные явления неоднократно наблюдались в лабораториях.

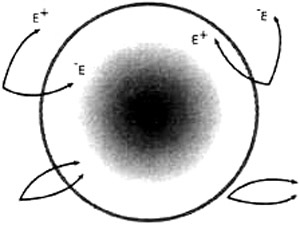
Именно квантовые флуктуации определяют процессы излучения черных дыр. Если пара частиц, обладающих энергиями E и –E (полная энергия пары равна нулю), возникает в окрестности сферы Шварцшильда, дальнейшая судьба частиц будет различной. Они могут аннигилировать почти сразу же или вместе уйти под горизонт событий. При этом состояние черной дыры не изменится. Но если под горизонт уйдет только одна частица, наблюдатель зарегистрирует другую, и ему будет казаться, что ее породила черная дыра. При этом черная дыра, поглотившая частицу с энергией –E, уменьшит свою энергию, а с энергией E – увеличит.

В мощном поле тяготения черной дыры происходит рождение пар частица-античастица. Поглощение частиц с отрицательной энергией приводит к уменьшению полной энергии черной дыры – ее испарению.

Хокинг подсчитал скорости, с которыми идут все эти процессы, и пришел к выводу: вероятность поглощения частиц с отрицательной энергией выше. Это значит, что черная дыра теряет энергию и массу – испаряется. Кроме того она излучает как абсолютно черное тело с температурой T = 6 ·10 ^– 8 M_с / M кельвинов, где M_с – масса Солнца (2 ·10 ³³ г), M – масса черной дыры. Эта несложная зависимость показывает, что температура черной дыры с массой, в шесть раз превышающей солнечную, равна одной стомиллионной доле градуса. Ясно, что столь холодное тело практически ничего не излучает, и все приведенные выше рассуждения остаются в силе. Иное дело – мини-дыры. Легко увидеть, что при массе 10 ¹⁴ – 10 ³⁰ граммов они оказываются нагретыми до десятков тысяч градусов и раскалены добела! Следует, однако, сразу отметить, что противоречий со свойствами черных дыр здесь нет: это излучение испускается слоем над сферой Шварцшильда, а не под ней.

Рождение пары частица-античастица в лаборатории. Гамма-квант высокой энергии (он трека не оставляет и на снимке не виден) сталкивается с неподвижным электроном. При столкновении возникают электрон и позитрон, траектории которых магнитное поле закручивает в разные стороны, а электрон приобретает энергию и с большой скоростью улетает. Еще один гамма-квант порождает вторую электрон-позитронную пару (на снимке внизу).

Итак, черная дыра, которая казалась навеки застывшим объектом, рано или поздно исчезает, испарившись. Причем по мере того, как она «худеет», темп испарения нарастает, но все равно идет чрезвычайно долго. Подсчитано, что мини-дыры массой 10 ¹⁴ граммов, возникшие сразу после Большого взрыва 10 – 15 миллиардов лет назад, к нашему времени должны испариться полностью. На последнем этапе жизни их температура достигает колоссальной величины, поэтому продуктами испарения должны быть частицы чрезвычайно высокой энергии. Возможно, именно они порождают в атмосфере Земли широкие амосферные ливни – ШАЛы. Во всяком случае, происхождение частиц аномально высокой энергии – еще одна важная и интересная проблема, которая может быть вплотную связана с не менее захватывающими вопросами физики черных дыр.

* См. здесь: Подборка статей В. Л. Гинзбурга, приложение 10.5 (прим. вед. сайт).

** См. здесь: А. Голубев, В поисках гравитационных волн: проект ЛИГО (прим. вед. сайт).